初二数学竞赛测试题五

初二数学竞赛测试题五

班级　　　　　　　 姓名　　　 　 

一、　　　  选择题(每小题4分，共32分)

1．如果a＞b,则－b一定是（　　 ）

A、负数　　B、非负数　　C、正数　　  D、非正数。

2．已知x﹥0,y﹤0,∣x∣﹤∣y∣,则x+y是（　　）

A、零　　　B、正数　　　　C、负数　　D、不确定。

3．如图，△ABC中，∠B=∠C，D在BC边上，　　　∠BAD=50⁰，

在AC上取一点E，使得∠ADE=∠AED，则∠EDC的度数为（　 ）

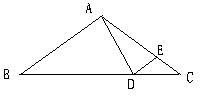A、15⁰　　　B、25⁰　　　 C、30⁰　　 D、50⁰ 

4．满足等式

 

的正整数对（x,y）的个数是（　　  ）

A、1　　　B、2　　　　 C、3　　　 D、4

5．今有四个命题：

①　  若两实数的和与积都是奇数，则这两数都是奇数。

②　  若两实数的和与积都是偶数，则这两数都是偶数。

③　  若两实数的和与积都是有理数，则这两数都是有理数。

④　  若两实数的和与积都是无理数，则这两数都是无理数。

其中正确命题个数为（　）

A、0　　　B、1　　　　 C、2　　　 D、4

6．若M=3x²-8xy+9y²-4x+6y+13（x,y是实数），则M的值一定是（　　　）

A、正数　　 B、负数　　  C、零　　　 D、整数

7．设A=48则与A最接近的正整数是（　　 ）

A、18　　B、20　　 C、24　　 D、25

8.如果关于x的方程k(k+1) (k-2)x²－2(k+1) (k+2)x+k+2=0,只有一个实数解,则实数k可取不同的值的个数为(　　)

(A)2　　　(B)3　　(C)4　　 (D)5.

二.填空题(每小题5 分共30分)

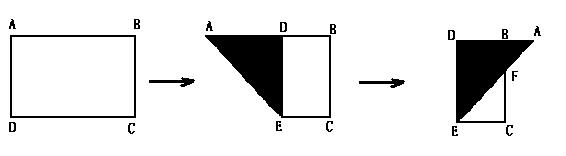9．如图,有一块矩形ABCD,AB=8,AD=6.将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向上翻折,AE与BC的交点为F,则△CEF的面积为　　　　  .

10．关于x的方程∣∣x-2 ∣－1∣=a有三个整数解，则a的值是　　　　.

11．已知关于x的方程a²x²－(3a²－8a)x+2a²－13a+15=0(其中a是非负整数)，至少有一个整数根，那么a= 　　　　　　.

12．若关于x的方程有增根x=－1,则a=　　　　　 . 　　　 

13．已知三个质数a,b,c满足a+b+c+abc=99,那么=　　.　　　

14.在一个圆形时钟的表面,OA表示秒针,OB表示分针(O为两针的旋转中心).若现在时间恰好是12点整,则经过　　　 秒钟后,△OAB的面积第一次达到最大.　　　　 

二、　　　  解答题

15．如图已知△ABC中，∠ACB=90⁰,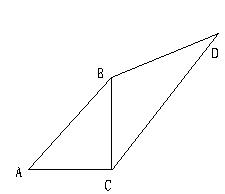 　　　　　　　　　　　

AC=BC，CD∥AB，BD=AB，　　　　　　　

求∠D的度数。（13分）

　　　　　　　　　　　　　　　　　　　　 

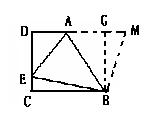
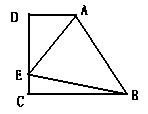16.如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90⁰,

BC=CD=12, ∠ABE=45⁰,若AE=10,求CE的长. （15分）

 

17.欣欣农工公司生产一种绿色蔬菜，若在市场上直接销售，每吨利润为1000元，经粗加工后销售，每吨利润可达4500元，经精加工后销售，每吨的利润涨至7500元。

欣欣农工公司收获这种蔬菜140吨，该公司的生产能力是如果对蔬菜进行粗加工，每天可加工16 吨，如果进行精加工，每天可以加工6 吨，但两种加工方式不能同时进行。受季节等条件限制，公司必须用15天的时间将这批蔬菜全部销售或加工完毕，因此，公司研制了三种可行方案：

(1)：将蔬菜全部进行粗加工；

(2)：尽可能多的对蔬菜进行精加工，没来得及进行加工的蔬菜，在市场上直接销售。

(3)：将一部分蔬菜进行精加工，其余蔬菜进行粗加工，并恰好用15天完成。

你认为选择哪种方案获利最多？为什么? （15分）

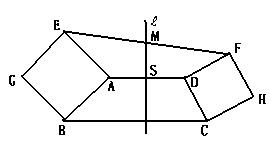18．已知,如图,梯形ABCD中,AD∥BC,

以腰AB、CD为一边分别向两边作正方

形ABGE和DCHF，设线段AD的垂直平分

线交线段EF于点M.

求证:M是EF的中点. （15分）

参考答案：

一、CCBB（左边因式分解：（，而>0,所以,xy=2003,因为2003是质数，必有x=1,y=2003或x=2003,y=1）AA(M=2(x-2y)²+(x-2)²+(y+3)²≥0且x-2y,x-2,+3不同时为0，所以M>0)D(对于正整数n≥3,有所以A=48=48=12=25-12

因为12<12<所以与A最接近的数为25.Ck=0,k=,△=0,得k=-2,k=-.

二、9.由折叠过程可知：DE=AD=6，∠DAE=∠CEF=45⁰，所以△CEF是等腰直角三角形，且CE=8-6=2，所以S_△CEF=2；10.1；11、1，3，5；12、3；13、三质数不可能都是奇数，则必有一个为偶质数2；若a=2，代入得b+c+2bc=97,同理b,c不可能都奇，若b=2,则c=19,所以原式为34；14、设OA边上的高为h，则h≤OB,当OA⊥OB时，等号成立，此时△OAB的面积最大；设t秒时，OA与OB第一次垂直，又因为秒针1秒钟旋转6度，分针1秒钟旋转0.1度，于是

（6-0．1）t=90，解得：t=.

15、解：作DE⊥CD于E，CF⊥AB则DE=CF=AB=BD，故∠D=30⁰。

16．延长DA至，使BM⊥BE，过B作BG⊥AM，G为垂足，

知四边形BCDG为正方形，所以BC=BG，∠CBE=∠GBM

∴Rt△BEC≌Rt△BMG　∴BM=BE，∠ABE=∠ABM=45⁰

∴△ABEC≌△ABM　 ∴AM=AE=10

设CE=x，则AG=10-x，AD=12-（10-x）=2+x,DE=12-x

AE²=AD²+DE²　 ∴100=(2+x)²+(12-x)²　即x²-10x+24=0

解得；x₁=4,　x₂=6∴CE=4或6。

17．解(1)设将蔬菜全部进行粗加工,获利W₁元

则W₁=1404500=630000元.

(2)设尽可能多的对蔬菜进行精加工，没来得及进行加工的蔬菜，在市场上直接销售, 获利W₂元

则W₂=1567500+(140-156) 1000=72500元.

(3) 设蔬菜进行精加工x天，其余蔬菜进行粗加工y天,获利W₃元

则　 解得:　

W₃=5164500+1067500=855000元

故选择方案三获利最多.

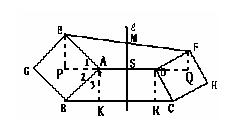
18．作EP⊥DA，FQ⊥DA，AK⊥BC，DR⊥BC，

可知AK=DR，AS=SD。

Rt△ABK≌Rt△AEP　 AP=AK

同理：Rt△DRC≌Rt△DQF　 DR=DQ　S是PQ的中点

PS=QS　∵EP∥SM∥QF　∴EM=MF　即M是EF的中点。