2006年春季期中试卷
八年级 数学 总分120分 得分
一.填空题(3分×10=30分)
1.当k= 时,y=(2k+2)xk-2为反比例函数,此时它的图象在第 象限内,当x>0时y随x的减小而 。
2.下列各式①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中是分式的是 (填序号)。
,其中是分式的是 (填序号)。
3.化简![]() 的结果是
。
的结果是
。
 4.当分式
4.当分式![]() 的值为零时,x的值是 。
的值为零时,x的值是 。
5.若y与![]() 成正比例,x与
成正比例,x与![]() 成反比例,则y与z成
比例。
成反比例,则y与z成
比例。
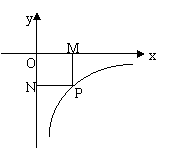
6.如图,已知点P是反比例函数y=![]() 的图象在第四象限内一
的图象在第四象限内一
点,过P点分别作x轴,y轴的垂线,垂足分别为M、N,若
矩形OMPN的面积为5,则反比例函数解析式为 。
7.已知直角三角形两边长分别为3cm、4cm,则此三角形面积为 。
8.已知x=![]() ,xy=1,则分式
,xy=1,则分式![]() 的值为 。
的值为 。
9.若点P在y=-![]() 的图象上,A点的坐标(0,2),点B坐标为(0,-2),且S△PAB=6,则
的图象上,A点的坐标(0,2),点B坐标为(0,-2),且S△PAB=6,则
P点坐标为 。
10.方程x+![]() =4
=4![]() 的解是 。
的解是 。
二.选择题(3分×8=24分)
1.下列等式中,哪个等式表示y是x的反比例函数( )
A、y=![]() B、y=
B、y=![]() C、y=
C、y=![]() D、2xy=1
D、2xy=1
 2.如果A(a1,b1)与B(a2,b2)在双曲线y=
2.如果A(a1,b1)与B(a2,b2)在双曲线y=![]() 的同一分支上,且a1<a2,则b1、b2的大小关系是( )
的同一分支上,且a1<a2,则b1、b2的大小关系是( )
A、b1﹤b2 B 、b1=b2 C 、b1>b2 D、不能确定
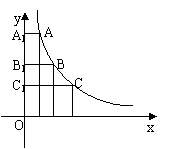
3.在函数y=的图象上有三点A、B、C,由这三点分别向
x轴、y轴作垂线,若矩形AA1OA2、BB10B2、CC1OC2的面
积分别为SA、SB、SC、,则下列结论正确的是( )
A、SA>SB>SC B、SA≥SB≥SC
C、SA<SB<SC D、SA=SB=SC
4.甲、乙两队分别从A、B两地同时出发,若相向而行,则a小时相遇,若同向而行,则b小时甲追上乙,那么甲的速度是乙的多少倍( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5.已知反比例函数y=![]() 的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有
的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有
y1<y2,则m的取值范围是( )
A、m<1 B、m>1 C、m>2 D、m<2
6.若直角三角形的三边长分别为2、4、x,则x的可能值有( )
A、1个 B、2个 C、3个 D、4个
 7.直角三角形中,周长为2+
7.直角三角形中,周长为2+![]() ,斜边上的中线为1,
,斜边上的中线为1,
则此直角三角形的面积为( )
A、2 B、 C、4 D、
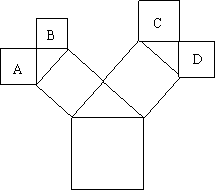
8.如图所示的图形中,所有的四边形都是正方形,
所有的三角形都是直角三角形,其中最大的正方
形的边长为7cm,则正方形A、B、C、D的面积的和是( )
A、25cm2 B、16cm2 C、36cm2 D、49cm2
三.解答下列各题:
1. 已知a=![]() ,写出用a的代数式表示b的推理过程。(6分)
,写出用a的代数式表示b的推理过程。(6分)
2. 化简并求值(7分)
(x-1-![]() )÷
)÷![]() ,其中x=3-
,其中x=3-![]()
3. 已知a=![]() ,求
,求![]() -
-![]() 的值。(7分)
的值。(7分)
4.  三角形的面积为6cm2。(8分)
三角形的面积为6cm2。(8分)
⑴求底边上的高ycm与底边xcm之间的函数关系式。
⑵作出这个函数的图象。
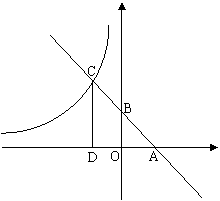 5.(7分)如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(m≠0)的图象在第二象限交于C点,CD垂直于x轴,垂足为D,若OA=OB=OC=OD=1。
5.(7分)如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(m≠0)的图象在第二象限交于C点,CD垂直于x轴,垂足为D,若OA=OB=OC=OD=1。
⑴求点、A、B、D的坐标。
⑵求一次函数和反比例函数的解析式。
6. 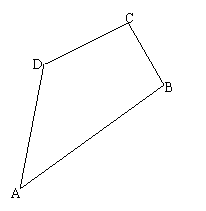 已知四边形ABCD中,∠C=90°,AB=25,BC=9,CD=12,AD=20,求四边形ABCD的面积。(9分)
已知四边形ABCD中,∠C=90°,AB=25,BC=9,CD=12,AD=20,求四边形ABCD的面积。(9分)
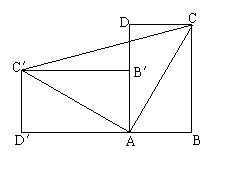 7.一个直立的火柴盒在桌面上到下,启迪人们发现了勾股定理的一种新的证明方法,如图火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积证明勾股定理:a2+b2=c2.(10分)
7.一个直立的火柴盒在桌面上到下,启迪人们发现了勾股定理的一种新的证明方法,如图火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积证明勾股定理:a2+b2=c2.(10分)
8.⑴如表,方程1、方程2、方程3……,是按照一定规律排列的一列方程,解方程1,并将它的接填在空白处.(3分)
⑵若方程=1(a>b)的解是x1=6,x2=10,求a、b的值.(3分)
⑶请写出这列方程中的第n个方程和它的解,并验证写出的解适合第n个方程.(6分)
| 序号 | 方程 | 方程的解 |
| 1 |
| x1= ,x2= |
| 2 |
| x1=4, x2=6 |
| 3 |
| x1=5, x2=8 |
| …… | …… | …… |