1.5~1.6 一元一次不等式与一次函数、一元一次不等式组(A卷)
班级：_______姓名：_______得分：_______发展性评语：___________
一、请准确填空(每小题3分，共24分)
1.不等式组
的整数解是________.
答案－1、0:
2.某含有x的不等式组的解集在数轴上表示如图1，则此不等式的解集应写为________.
图1
答案:－2≤x＜1
3.若点A(－1，y1)、B(2，y2)都在直线y=－x+
上，则y1与y2的关系是________.
答案:y1＞y2
4.当x满足条件______时，不等式2x+3>0与x－3<0同时成立.
答案:－
＜x＜3
5.对于一次函数y=x+6，当x______时，y>0；当x______时，y=0；当x______时，y<0.
答案:＞－4 =－4 ＜－4
6.若方程mx+2=x－4的解是负数，则m的取值范围是______.
答案:m＞1
7.想一想，请写出一个不等式组，其整数解为5，则该不等式组为______.
答案:
(不唯一)
8.小亮每小时能走4千米，他出发两小时后，让你骑车在30分钟内追上小亮，猜想你骑车必须每小时至少走________千米.
答案:20
二、相信你的选择(每小题3分，共24分)
9.不等式组
的解集是
A.x<3 B.－2<x<3 C.x>－2 D.x>3或x<－2
答案:B
10.在一次函数y=4x－5中，若y>11，则
A.x>4 B.x> C.x<4 D.x>
答案:A
11.下列四个图形中表示解集－3≤x<1的是
图2
答案:C
12.一元一次不等式组
(a≠b)，若它的解集是a<x<b，则a与b满足
A.a>b>0 B.a<b C.a>b D.a<b<0
答案:B
13.若不等式组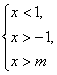
无解，则m的取值范围是
A.m≤－1 B.m≥1 C.－1<m<1 D.m≤－1或m≥1
答案:D
14.已知一次函数y=mx+2x－1，要使y的值随x值的增大而增大，则m应满足
A.m≥－2 B.m≤－2 C.m>－2 D.m<－2
答案:C
15.已知关于x的不等式x≤a的正整数解为1，2，3，则a的取值范围是
A.a≤3 B.a=3 C.a<4 D.3≤a<4
答案:D
16.图3所示的是甲、乙两同学在一次赛跑中，路程s与时间t之间的关系图象，则下列说法错误的是
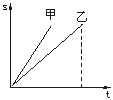
图3
A.乙比甲跑的慢 B.乙比甲跑的路程多
C.甲比乙先到终点 D.甲、乙同时出发
答案:B
三、考查你的基本功（共20分）
17.（10分）解不等式组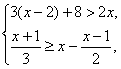
并把解集在数轴上表示出来.
答案:－2＜x≤－1，数轴略.
18.（10分）已知
，且a>2>b，请探求x的取值范围.
解：∵a＞2＞b，∴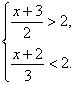
解得
∴1＜x＜4.
四、生活中的数学(共20分)
19.（10分）甲、乙两辆客车分别从相距40千米的A、B两地同时相向而行.如图4所示，l1、l2分别表示甲、乙两辆客车离开A地、B地的路程s（千米）与时间t(小时)之间的函数关系.（精确到0.01）
（1）甲、乙两辆客车哪辆车的速度快？你是怎样知道的？
（2）两车相遇时，两车行驶了多长时间？甲车距B地还有多少千米？
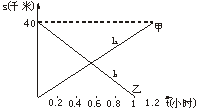
图4
解：(1)乙车的速度快，因为在40千米内，乙比甲用的时间少.
甲车速
=33.33千米/时.
乙车速
=40千米/时.
(2)设相遇时两车行驶了x 小时，
则有x+40x=40，即2.2x=1.2. ∴x≈0.55(h).
故甲车距 B 地的路程为40－×0.55≈21.68千米.
20.（10分）在爆破时，如果导火索燃烧的速度是每秒钟0.5厘米，人跑开的速度是每秒钟4米，为了使点燃导火索的人在爆破时能跑到100米以外的安全地区，导火索的长度至少要多长？
解：设需导火索至少x米，
依题意得
≥
.
∴x≥0.125(米)=12.5(厘米).
答：导火索至少要12.5厘米，人才能到达安全区.
五、探究拓展与应用（共12分）
21.某校5名教师要带若干名学生到外地参加一次科技活动.已知每张车票价格是120元，购车票时，车站提出两种优惠方案供学校选择.甲种方案是：教师按车票价格付款，学生按车票价格的60%付款；乙种方案是：师生都按车票价格的70%付款.请你根据参加活动的学生人数的变化，设计一套比较优惠的方案，并与同学交流.
解：设有x 名学生参加.
则甲种方案付款5×120+120×60％·x=600+72x.
乙种方案付款(x+5)×120×70％=84(x+5).
(1)当600+72x=84(x+5)时，x=15，
即有15名学生时，两种方案付款一样.
(2)当600+72x＜84(x+5)，
即x＞15时，有15名以上学生时，甲种方案付款较少.
(3)当600+72x＞84(x+5)时，x＜15.
即学生数少于15人时，乙种方案付款较少.