毕宏中学八年级上学期数学期中试卷
一、填空（10×3分）
1、
菱形的面积是3
,一条对角线的长度是3cm，另一条对角线的长是_________cm。
2、 若等腰梯形一个内角为75°,则其余三个角的度数为_________________。
3、
如图，矩形ABCD的长为6cm，宽为4cm，O是对称中心，则图中阴影部分的面积是_________。
4、 如图，矩形ABCD的周长是24，M是BC的中心，∠AMD=90°，则矩形相邻两边的长分别是__________。
5、 请你写一条菱形具有而平形四边形不具有的性质：____________（只要写出一条即可）。
6、 如图，△ABC为等边三角形，D为△ABC内一点，△ABD经过旋转后到达△ACP的位置。（1）旋转中心为______；（2）旋转角度为_____；（3）△ADP是_____三角形。
7、 矩形的一条对角线与较长的边相交成30°角，较短的一条边与一条对角线之和为24cm，则矩形对角线长为_______cm。
8、
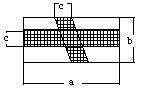
如图,过矩形ABCD对角线BD上一点K分别作矩形两边的平行线MN和PQ，那么图中矩形AMKP的面积
与矩形QCNK的面积
的大小关系是____（填写“>”或“<”、“=”）。
9、 如图，△ABC中，∠C=90°，AC=BC，点G、F分别在AC、BC上，点D、E在AB上，且DG丄EF，OG=OD=OE=OF，若GF=a，则AB=___________。
10、如图，把矩形纸片沿对角线AC折叠，使B点落在
处，
交DC于E点，∠
=146°，∠EAC=______度。
二、选择题（15×3分）
1、下列运动属于平移的是（ ）
A、 冷水加热过程中小气泡上升成大气泡 B、打开教室门，门的移动
C、上升的电梯
D、随风飘动的风筝在空中运动
2、在矩形ABCD中横向阴影部分为矩形，另一阴影部分为平行四边形，依照图中标注的数据计算图中空白部分面积为（ ）
A、
B、
C、
D、
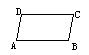3、如图，在平行四边形ABCD中，若∠B=100°，那么∠A、∠D的度数分别是（ ）度
A、80、100 B、100、80 C、80、80 D、100、100
4、已知
ABCD，下列判断正确的是（ ）
A、若∠A=90°，则四边形ABCD是矩形 B、AC=BD
C、AB=CD，则ABCD是菱形 D、若AC丄BD，则四边形ABCD为正方形
5、在平行四边形ABCD中，∠A：∠B：∠C：∠D的值可以是（ ）
A、1:2:3:4 B、3:4:4:3 C、3:3:4:4 D、3:4:3:4
6、要使正八边形旋转后自身重合，至少应将它绕中心顺时针方向旋转的度数为（ ）度
A、30 B、45 C、60 D、135
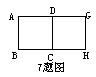
7、如图相同的两块正方形铁皮ABCD与DCHG，要使它们重合，存在的旋转中心有（ ）个
A、0 B、1 C、2 D、3
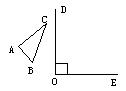8、如图，∠DOE为直角，如果△ABC关于OD的对称图形是△
,△关于OE对称图形是△
,则△ABC与△的关系是（ ）
A、以∠DOE的平分线成轴对称 B、关于点O成中心对称
C、平移关系 D、不具备任何关系
9、a的3倍与9的和不小于15，用不等式表示为（ ）
A、3a+9>15 B、3(a+9)>15 C、3a+9≥15 D、3(a+9)≥15
10、当x=1时，下列不等式成立的是（ ）
A、x+3>4 B、x-2<1 C、x+1>2 D、x-1<0
11、解不等式
的下列过程，错误之处是（ ）
A、5(2+x)>3(2x-1) B、10+5x>6x-3 C、5x-6x>-3-10 D、x>13
12、关于x的不等式(n-m)x>0，其中m>n，则它的解集是（ ）
A、x>0 B、x<0 C、x>n-m D、x>m-n
13、已知：矩形一个角的平分线把一边分为4cm和5cm两部分，则这个矩形的周长为（ ）
A、26cm B、27cm C、27cm和29cm D、26cm和28cm
14、在下列图形中：①线段②角③圆④等边三角形⑤正五边形⑥正方形⑦平行四边形⑧矩形⑨菱形，既是中心对称图形，又是轴对称图形的是（ ）
A、①④⑤⑥⑧⑨ B、①③⑥⑧⑨ C、②③⑦⑧ D、②④⑤⑨
15、四边形ABCD的对角线AC、BC相交于O，设有下列条件：①AB=AD；②∠DAB=90°；③BO=DO，AO=CO；④矩形ABCD；⑤菱形ABCD；⑥正方形ABCD，则下列推理不成立的是（ ）
A ① ⑥ B ①
⑤ C ①
⑥
D ② ④
④ ③ ② ③
三、解答题（4×5分）
1、
解不等式
的最小整数解是方程
的解，求a的值。
2、 作图题
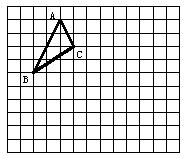在下面的网格中先画出△ABC向下平移5格的△
,再画出△ABC以点O为旋转中心，沿顺时针方向旋转90°后的△
。
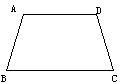
3、 如图，等腰梯形ABCD中，AD∥BC，AB=DC，∠B=60°，AD=3cm，DC=5cm，求梯形ABCD的周长。
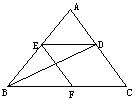
4、 如图，已知△ABC中，BD是ABC的平分线，DE∥BC，EF∥AC，试说明，BE=FC。
四、（2×6分）
1、 四边形ABCD中，分别过A、B、C、D，作对角线BD，AC的平行线，两两相交于E、F、G、H。
（1） 画出图形，并识别四边形EFGH的形状：______________。
（2） 当四边形ABCD满足________时，四边形EFGH为菱形；
（3） 当四边形ABCD满足________________时，四边形EFGH为正方形。（注意：在横线上补充你认为必要的条件）
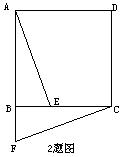
2、 如图所示，正方形ABCD中，E为BC边上一点，将△ABE旋转后得到△CBF。
（1） 指出旋转中心及旋转的角度。（2）判断AE与CF的位置关系。
（3）如果正方形的面积是18，△BCF的面积是5，问四边形AECD的面积是多少？
五、（1小题6分，2小题7分，共13分）
1、
已知：ABCD的周长为28cm，对角线AC与BD的长度之比为2:3，△AOB与△OBC的周长和为34cm，求AC和BD的长。
2、 如图所示，梯形ABCD中，AD∥BC，∠B=90°，AB=14cm，AD=18cm，BC=21cm，点P从点A开始沿AD边向点D以1cm/秒的速度移动，点Q从点C开始沿CB向点B以2cm/秒的速度移动，如果P、Q分别从A、C同时出发，设移动时间为t秒。
（1）
当t为何值时，四边形PDCQ是平行四边形？
（2） 当t为何值时，四边形PDCQ是等腰梯形？