初二（上）综合复习二
(A卷 共100分)
一、选择题（4×10分）
1、下列各点①（－3，2）②（1，1）③（0，0）④（3，3－
）在函数
y=x－
的图象上的是（ ）
A、①② B、①③ C、②③ D、②④
2、已知a的算术平方根是8，则a的立方根是（ ）
A、±2 B、±4 C、2 D、4
3、若x＜2，化简
＋3－x正确的是（ ）
A、－1 B、1 C、2x－5 D、5－2x
4、在直角坐标系中，若一图形的横坐标不变，纵坐标分别减去2，
所得图形与原图形相比（ ）
A、 向上平移2个单位长度
B、 向右平移2个单位长度
C、 向左平移2个单位长度
D、 向下平移2个单位长度
5、对于数组3，3，2，3，6，3，10，3，6，3，2，其正确的结论是（ ）
A、中位数是3 B、众数与中位数的值不相等
C、中位数与平均数值相等 D、平均数与众位数的值相等
6、下列说法正确的是（ ）
A、 四条边都相等的四边形是正方形
B、 四个角都相等的四边形是正方形
C、 对角线相等的菱形是正方形
D、 一条对角线平分一组对角的四边形是菱形
7、若方程ax－3y=2有一个解是
则a的值为
（ ）
A、－8 B、8 C、－4 D、4
8．下列图案中既是中心对称图形，又是轴对称图形的是( )
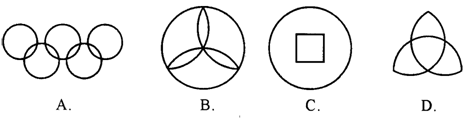
9、函数
的自变量x的取值范围是( )
A．
B．
C．
D．
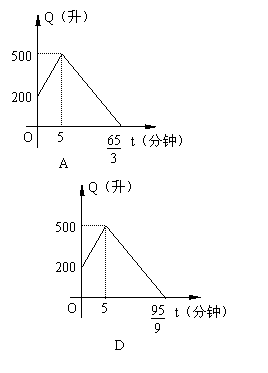
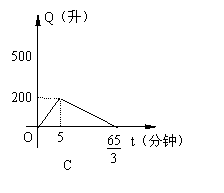
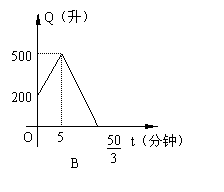10、有一个装有进、出水管的容器，单位时间年7进、出的水量都是一定的。已知容器的容积为600升，又知单开进水管10分钟可把空容器注满，若同时打开进、出水管，20分钟可把满容器的水放完，现已知水池内有水200升，先打开进水管5分钟后，再打开出水管，两管同时开放，直至把容器中的水放完，则能正确反映这一过程中容器的水量Q（升）随时间t（分）变化的图象是（
）
 | |||
 | |||
二、填空题（3×8分）
1、请写出一个图象经过点（１，４）的函数解析式：________.
2、正六边形的一个内角的度数是___________º
3、已知
，则
_________；
4、在平面直角坐标系中，点P（2，5）关于原点的对称点P’的坐标在
第 象限
5、在实数－2，
，0，－1.2，
中，无理数是 。
6、在航天知识竞赛中，包括甲同学在内的6名同学的平均分为74分，其中甲同学考了89分，则除甲以外的5名同学的平均分为 分
7、已知菱形的周长为20cm,两条对角线之比为3：4，则菱形的面积为________
8、已知x、y为实数，且+ 3（y – 2）2 = 0，则x – y的值为
三、计算：（6分） 
.
四、（6分）解方程组：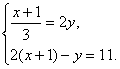
五、 （6分） 已知一次函数y=（3m－7）x＋m－1的图象与y轴的交点在x轴的上方，且y随x的增大而减小，m为整数，求此函数的表达式
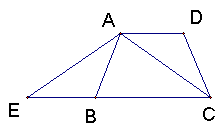五、（8分）如图，梯形ABCD中，AD∥BC，AB=CD，延长CB至E，使EB=AD，试探究
AE和AC间有何数量关系,说明理由.
六、（8分）小明的爷爷退休生活可丰富了!下表是他某日的活动安排.和平广场位于爷爷家东400米,老年大学位于爷爷家西600米.从爷爷家到和平路小学需先向南走300米,再向西走400米.
(1)请依据图示中给定的单位长度,在图中标出和平广场A、老年大学B与和平路小学的位置.
(2)求爷爷家到和平路小学的直线距离.
| 早晨6:00—7:00 与奶奶一起到和平广场锻炼 |
| 上午9:00—11:00 与奶奶一起上老年大学 |
| 下午4:30—5:30 到和平路小学讲校史 |
(B卷 共50分)
一、 填空题（3×5分）
1、写出一个图象经过点(-1,-1),且不经过第一象限的函数表达式______.
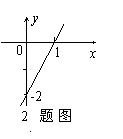2、已知一次函数y=kx+b的图象（如图），当x＞0时，
y的取值范围是
3、根式
是同类二次根式，
则
___________.
4、、点A（3，－5）关于y轴的对称点为B，关于y轴的对称点为C，则BC直线方程是
5、图中的螺旋形由一系列直角三角形组成，
则第n个三角形的面积为 。
二、（6分）已知y=y1+y2，y1与x成正比例，y2与2x－1成正比例，并且x=2时与x=3时，y值都是9，求y与x间的函数关系式
三、（6分）列方程或方程组解应用题：
东方食品厂2003年的利润（总产值-总支出）为200万元，2004年总产值比2003年增加了20%，总支出减少了10%。2004年的利润为780万元。问2003年总产值、总支出各是多少万元？
四、（7分）随着海峡两岸交流日益增强，通过“零关税”进入我市的一种台湾水果，其进货成本是每吨0.5万元，这种水果市场上的销售量
（吨）是每吨的销售价
（万元）的一次函数，且
时，
；
时，
。
（1）求出销售量（吨）与每吨的销售价（万元）之间的函数关系式；
（2）若销售利润为
（万元），请写出与之间的函数关系式，并求出销售价为每吨2万元时的销售利润。
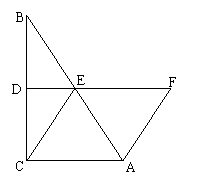五、（7分）如图，在Rt△ABC中，∠ACB = 90°，∠BAC = 60°，DE垂直平分BC，垂足为D，交AB于点E。又点F在DE的延长线上，且AF = CE。请你判断四边形ACEF是何特殊四边形，
说明理由。
六、（9分）一天上午6点钟，汪老师从学校出发，乘车上市里开会，8点准时到会场，中午12点钟回到学校，他这一段时间内的行程S（km）（即离开学校的距离）与时间（h）的关系可用图4中的折线表示，根据图4提供的有关信息，解答下列问题：
（1）开会地点离学校多远？
（2）求出汪老师在返校途中路程S（km）与时间t（h）的函数关系式；
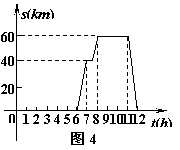（3）请你用一段简短的话，对汪老师从上午6点到中午12点的活动情况进行描述．