八年级数学期中综合
一、选择题：
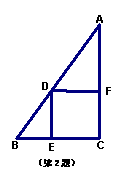
1、已知：如图，四边形ABCD中∠B=∠D=90°，
∠C=45°，AD=3㎝，BC=7㎝，则四边形
ABCD的面积是 ㎝2.
2、已知：如图，Rt△ABC中∠C=90°，点D、
E和F分别在AB、BC和AC上，且四边形
DECF为正方形，若AD=6cm，BD=4cm，
则△ADF与△DBE的面积和：S△ADF+S△DBE是 cm2
二、填空题：
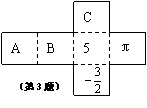3、如图,是一个正方体纸盒展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,则A,B,C表示的数依次是(
)
A. 
B. 
C.
D. 
4、2008年8月，在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一
个大正方形（如图）.如果大正方形的面积是13，小正方形的面
积是1，直角三角形的较短直角边为a. 较长直角边为b，那么
（a+b）2的值为 ( )
A、 19 B、13 C、25 D、169
5、已知：如图，正方形
的边长为4，现沿对角线所在直线
向右平移与
正方形
重合，已知四边形
的面积为1，则
的长度为（
）
（A）
（B）
（C）
（D）
三、解答题：
6、如图，在直线MN上能否找到点A，使以BC
为一边的△ABC是等腰三角形，如果能的话，
试着把它找出，并把它画出来.
7、已知：一列数据x1，x2，x3，…，xn-1，xn的平均数
=
，
方差s2=
.
由此可以得出新数据x1+a，x2+a，x3+a，…，xn-1+a，xn+a的平均为+a，方差为s2.
相应的说明和理由如下：
∵
=
=
而=
∴上式=+a，即新数据的平均数为+a
又∵
=
而=s2
∴上式= s2，即新数据的方差为s2
(1) 参照上述的方法，来说明一例新数据bx1，bx2，bx3，…，bxn-1，bxn的平均数为b，方差为bs2，并写出相应的过程和理由.
(2) 若数据x1，x2，x3，…，xn-1，xn的平均数为2，==2，
方差s2==3.
结合上述的说明和解决问题的过程，请直接写出一例新数据2x1+3，2x2+3，2x3+3，…，2xn-1+3，2xn+1+3，的平均数为和方差（不必写出过程，直接写出相应的结果）.