（华师大）八年级数学第一学期期末测试题
一、选择题（10×4分=40分）
1、下列运算正确的是 ( )
A、
B、2a+3b=5ab C、
=
D、
2、下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A
B 
C 
D
3、如图，天平右盘中的每个砝码的质量都是1克，则图中物体M的质量范围是（ ）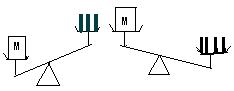
A、大于3克 B、小于4克 C、大于3克或小于4克 D、大于3克且小于4克
4、如果等腰梯形的两底之差等于一腰，则该梯形的较小底角的度数是（ ）
A、45° B、30° C、60° D、75°
5、某辆汽车的车牌号码在水面的影像是“
”，则该车的实际号码是（ ）
A、69245D B、D24596 C、D24569 D、24569D
6、以不在同一直线上的三点A、B、C为顶点画平行四边形，一共可以画（ ）
A、4个 B、3个 C、2个 D、1个
7、使得等式
成立的字母a的值是（ ）
A、2 B、3 C、4 D、5
8、不等式组
的最小整数解是（ ）
A、3 B、4 C、0 D、-1
9、在不透明的袋中装有10个除颜色不同外，其余均相同的小球：其中白球5个；黄球3个；红球2个。摇匀后，如果从中任意摸出一个球，那么摸出的球是白色或红球的机会大小是（ ）
A、0.5 B、0.2 C、0.3 D、0.7
10、小明在设计一种平面（镶嵌）图案时，因不小心将墨水瓶打翻，把设计的部分图案污染（如右图），则图中最下一行的图案（被墨水污染部分）应是（ ）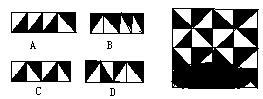
二、填空题（5×4分=20分）
11、从一副除掉大小王的52张扑克中，任意抽出一张，抽出的恰好是红桃的机会大小是
。
12、若
。
13、如果方程2a-3x=6的解是正数，则实数a的取值范围是 。
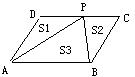
14、如图，点P为平行四边形ABCD的边CD上一点，则△APD、△BCP和△ABP的面积
之间的关系是
。
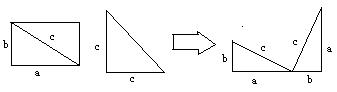15、如图，把长、宽、对角线的长分别是a、b、c的矩形沿对角线剪开，与一个直角边长为c的等腰直角三角形拼接成右边的图形，用面积割补法能够得到的一个等式是
。
三、（4×8分=32分）
16、解方程：
17、解不等式组：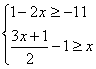
18、已知a+b=4,ab=3,求
得值。
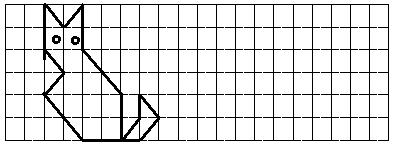
19、如图，画出猫向后平移8格后的图象。
四、（2×10分=20分）
20、我国是水资源缺乏国家之一，为节约用水，某地果园灌水采用喷头灌水技术（形如喷泉）：当灌水喷头的喷嘴直径为d（㎝），喷头的压强为g（kPa)时，喷化指标p=
。经实验得知：对某种果树灌水时要求3000≤p≤4000，若采用的喷头直径d=4㎝，那么喷头的压强g的取值范围是多少？
21、如图，已知等腰梯形ABCD中，AD∥BC，AD=2，BC=5，∠B=60°，求梯形ABCD的周长。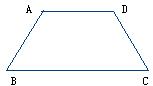
五、（本题满分12分）
22、如图，矩形ABCD的对角线AC、BD相交于点O，若把矩形ABCD用橡皮擦去一部分，变成右图，从中你发现什么现象？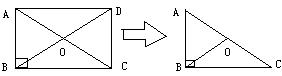
①请用语言表达你发现的规律；
②简单说明你发现的规律的正确性。
六、（本题满分12分）
23张华、李明、王莉同学用“红桃A、红桃2、红桃3”三张扑克牌做如下游戏。游戏规则：将三张扑克牌洗好后，每人从中摸出一张后再放回，张华如果摸出的是红桃A，则张华得1分；李明如果摸出的是红桃2，则李明得1分；王莉如果摸出的是红桃3，则王莉得1分；三个人如果摸出的不是自己所要的牌，一律得0分，以累计总分高的为胜。通过反复实验获得下表数据（每人都摸牌一次规定为一次实验）。
| 实验次数 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| 张华得分 | 57 | 39 | 98 | 130 | 168 | 204 | 233 | 267 | 299 | 334 |
| 李明得分 | 24 | 81 | 90 | 134 | 165 | 201 | 234 | 266 | 300 | 333 |
| 王莉得分 | 48 | 52 | 131 | 132 | 167 | 198 | 233 | 267 | 300 | 332 |
① 根据上述实验数据，完成下列频率统计表；
| 实验次数 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| 张华得分的频率（℅） | 57.0 | 19.5 | 32.6 | 32.5 | 33.6 | 34.0 | 33.4 | 33.2 | 33.4 | |
| 李明得分的频率（℅） | 24.0 | 40.5 | 30.0 | 33.5 | 33.0 | 33.5 | 33.4 | 33.3 | 33.3 | |
| 王莉得分的频率（℅） | 48.0 | 26.0 | 43.7 | 33.0 | 33.4 | 33.0 | 33.3 | 33.4 | 33.2 |
② 根据频率统计表中的数据，分别画出各人获胜的频率折线图；
③ 从频率统计表和三幅频率折线图中，你发现什么共同规律？请用一句形象的语言概括归纳出你发现的这个规律。
④ 通过观察各人获胜的频率折线图，猜想各人获胜的机会的大小（分别用一个数据表示）。
⑤ 你认为这个游戏规则公平吗？简单说出你的理由。
⑥ 如果你身边没有扑克牌，你能设计出一种借助替代物进行此种模拟实验的方法吗？简要说明这种模拟实验的方法和过程。
七、（本题满分14分）
24、阅读下列材料并回答问题：
我们知道，两数和的平方公式“
”可以用平面图形的面积来表示[如图（A）]。实际上，有些代数恒等式也可以用平面图形的面积表示，例如：（2a+b）(a+b)可以用图形（B）或（C）的面积表示。
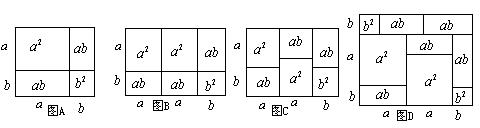
①请写出图形（D）所表示的一个代数恒等式： ；
②试画出一个平面图形，使它的木匠泥工表示代数恒等式：（a+b）(c+d)=ac+ad+bc+bd；
③请仿照上述方法另写出一个关于x、y的代数恒等式，并设计画出一个与之相对应的平面图形。（要求：与上述所列举的代数恒等式不同）