八年级第六章一次函数测试题
一填空题：
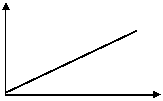
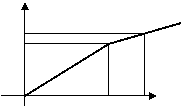
1、已知某晚报的售价是每份0.50元，y表示销售x份报纸的总价，则y与x的函数关系式是（ ）。若直线y=kx经过点（1，2），则k的值是（ ）
2、若函数y=（m—2）x+5—m是一次函数，则m满足的条件是（ ）若此函数是正比例函数，则m的值是（ ），若函数y=kx—4的图象平行于直线y=—2 x则函数的表达式是（ ）对于一次函数y=1—2x，y随着x的增大而（ ）
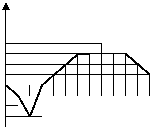3、如图是某地区一天的气温随时间变化的图象，根据图象回答
（1）t=（ ）时，气温最高，最高气温T=（ ）0C
（2）t=（ ）时，气温最低，最低气温T=（ ）0C
（3）在（ ）时段内，气温持续不变，
（4）在（
）段内，气温不断下降。
（5）晚上8点时，气温（ ）0C，（6）t=（ ）时，
气温达60C
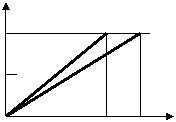
4、假定甲、乙在一次赛跑中，路程s与时间t的关系如图所示，
那么可以知道，（1）这是一次（ ）米赛跑，
（2）甲、乙两人中先到达终点的是（ ）
（3）乙在这次赛跑中的速度是（ ）。
二、选择题
1、下列说法不正确的是（ ）A 一次函数不一定是正比例函数。B 不是一次函数就一定不是正比例函数 C 正比例函数是特殊的一次函数，D 不是正比例函数就一定不是一次函数
2、若一次函数y=—x+b的图象经过点（0，-4）。则的值是（ ）A 1 B —1 C 4 D -4
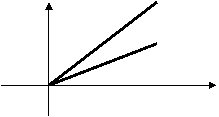3、下列函数中，y随x的增大而增大的函数是（
）
A y=2—x B y=—2x+1 C y=x—2 D y=—x—2
4、A、B两辆汽车均匀行驶的速度分别为VA、（千米/小时）和
VB（千米/小时），两辆汽车行驶的路程S（小时）与时间t（小时）
的函数关系图象分别是射线LA、TB如图所示（ ）
A VA= VB B VA＞VB C VA＜VB D VA≤VB
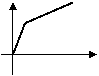
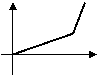
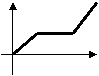
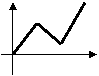5、李明骑车上学，一开始以某一速度行进，途中车子发生故障，只好停下来修车，车修好后，因怕迟到，于是加快了骑车的速度，在以下给出的四个函数图象中（S是距离，t是时间），符合以上情况的是（ ）
A B C D
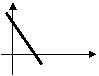
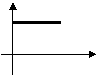
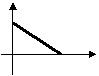
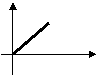
6、一根蜡烛长20cm，点燃后每小时燃烧5 cm，燃烧时剩下的高度h（cm）与燃烧时间t（小时）的函数关系用图象表示为（
）
A B C D
7、若一次函数y=2mx+（m2—2m）的图象经过坐标原点。则m的值为（ ）
A 2 B 0 C 0或2 D 无法确定
三、解答题 2、某地长途汽车客运公司规定旅客可随
1、 已知一次函数y=x+2，（1）在平面直角 身携带一定重量的行李，如果超过规
坐标系中画出函数的y=x+2的图象。（2）当x=2， 定，则需要买行李票，行李票费用y
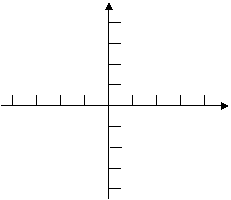
（3）观察图象，求当x取何值时，y＞0 （元）是行李重量x（千克）的一次函
数，其图象如下 ，（1）y与x的函数关
系式，（2）旅客最多可免费携带行李的
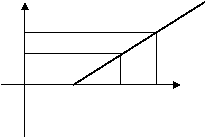千克数。
3、为了保护学生的视力，课桌椅的高度都是 4、某研究所开发一种新药，在检验药
按一定的关系配套设计的，研究表明：假设课 效时发现，如果成人按规定剂量服用，
桌的高度为y cm，椅子的高度为x cm，则y是x 那么服药2小时后血液中含药量较高，
的一次函数，下表列出 达到每毫升6微克，接着逐步衰减，服
|
| 第一套 | 第二套 |
| 椅子高度y cm | 40.0 | 37.0 |
| 桌子高度x cm | 75.0 | 70.2 |
药10小时后血液中含药量达每毫克3
微克，每毫升血液中含药量y（微克）
随着时间x（小时）的变化而变化如图
两套符合条件的课桌椅的高度
所示，（1）当成人按规定剂量服药后，
（1）请确定y与x的函数关系式。 别求出当 x≤2和x≥2时，y与x之间
（2）现有一把高42 cm的椅子和一张高78.2 的函数关系式。
cm的课桌，它们是否配套，请通过计算说明 （2）如果每毫升血液中含药量为4微克
理由。 或4微克以上时，治疗疾病的是有效的，
那么有效时间有多长？
 |
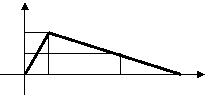5、A城有化肥200吨，B城化肥300吨，现要 6、某校餐厅计划购买12张餐桌和一批餐
将化肥运往C、D两地，如果从A城运往C、D 椅，现从甲、乙两商场了解到，同一
两地运费分别是20元/吨与25元/吨，从B城运往 型号的餐桌报价每张均为200元，餐
C、D两地运费分别是15元/吨与22元/吨，已知C 椅报价每把均为50元，甲商场称：每
地需要220吨，D地需要280吨，如果某个个体户 购买一张餐桌赠送一把餐椅；乙商场
承包了这项运输任务，请你帮他算一算，怎样调运 规定：所有餐桌椅均按报价的八五折
运费最少？ 销售，那么，什么情况下甲商场购买
更优惠？
八年级第六章一次函数测试题
一、
选择题
1、 小刚、爸爸、爷爷同时从家中
出发到达同一目的地后立即返回，
小刚去时骑自行车，返回时步行；
爷爷去时是步行，返回时骑自行车；爸爸往返都是步行，三个人步选择速度不等，小刚与爷爷骑车的速度相等，每个人行走的路程与时间的关系分别是如图所示中的一个，则走完一个往返，小刚用（ ）分钟，爸爸用（ ）分钟，爷爷用（ ）分钟。
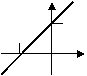
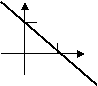
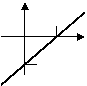2、在平面直角坐标系中，一次函数y=x+1的图象是
（ ）
A B C D
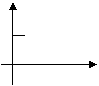3、某工厂去年积压产品a件（a＞0），今年预计每月销售2b件（b＞0），同时每月可生产出产品b件，若产品积压量y件是今年开工时间t（月）的函数，则其图象只能是图中的（ ）
 |  |  | |||
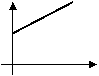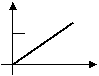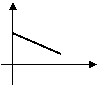A B C D
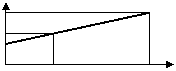
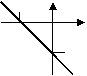
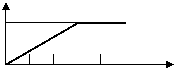4、弹簧的长度与所挂物体的质量的关系为一次函数，如图所示，则不挂物体时弹簧的长度为（
）cm。 A
7 B 8 C 9 D 10
 | |
5、一天，亮亮发烧了，早晨他烧的很厉害，吃过药后感觉好多了，中午时他的体温基本正常，但是下午报的体温又开始上升，直到半夜亮亮才感到身上不那么发烫了，下图中能基本反映出亮亮这一天体温的变化情况的是 （ ）
 |  |  | |
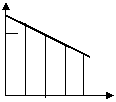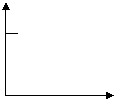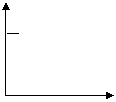二、 解答题
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1、如图表示一骑自行车者和一骑摩托车者沿相同路线从甲地到乙地行驶过程的函数图象，两地的距离是80千米，请根据图象回答下列问题：
（1）谁出发的早？早多长时间？谁到达乙地早？早多长时间？
（2）两人在途中的速度分别是多少？
（3）分别求出自行车和摩托车行驶过程的函数关系式。
2、一农民带了若干千克土豆进城出售，为了方便，他带子一些零钱备用，按市场价售出一些后，又降价出售，售出土豆怀他手中持有的钱数（含备用零钱）关系如图所示，结合图象回答下列问题，（1）农民自带的零钱是多少？（2）降价前他和线千克土豆卖多少元？（3）降价后他按每千克0。4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，问他一共带了多少千克土豆。
3、某商店钢笔每枝25元，笔记本每本5元，该店为促销制定了两种优惠方案：方案一：买一枝钢笔赠送一本笔记本；方案二：按购买总额的90%付款，（1）若某单位需要钢笔10枝，笔记本x（x≥10）本，则每种优惠方案的实际付款数y（元）是x的函数，表达式分别为
y1=（ ）y2=（ ）。（2）若某单位花495元购回了所需物品，问采作哪一种方案比较划算。（3）若可以任选一种方案，也可同时用两种方案购买，还可以在一优惠方法只买了一种物品，请你就购买10枝钢笔和60本笔记本设计一种最省钱的购买方案。
4、育英学校校办工厂生产了一批新产品，现有两种销售方案，方案一：在这学期开学时售出该批产品，可获利3000元，然后将该产品的成本（生产该批产品支出的总费用）和已获得的30000元进行再投资到这学期结束后，再投资又可获利4.8%；方案二：在这学期结束时售出该批产品，可获利35940元，但要付成本0.2%作保管费，设该批产品的成本为x（元）方案一的获利为y1元，方案二的获种为y2元，（1）分别求出y1，y2与x的函数关系式。（2）若该批产品的成本为80000元，方案一获利多少元？方案二获利多少元？（3）当该批产品的成本是多少元时，方案一与方案二的获利是一个的？（4）就成本x（元）讨论方案一好，还是方案二好。
5、 市为了鼓励市民节约用水，规定自来水的收费标准如下表。（1）已知胡老师家四月份用水18吨，则应缴水费多少元？（2）分别写出每月每户的水费y（元）与用水量x（吨）之间的函数关系式；（3）若已知胡老师家五月份的水费为17元，问他家五月份用水多少吨。
| 每月每户用水量 | 每吨价（元） |
| 不超过10吨部分 | 0.50 |
| 超过10吨不超过20吨部分 | 0.75 |
| 超过20吨部分 | 1.50 |