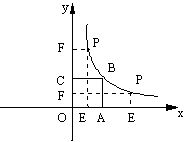外国语学校八年级(下)第一次阶段考试
数学试题
（时间：90分钟 总分：120分）
一、选择题（每小题3分，共30分）
1． 在
，
，
，
， 
＋
，9 x +
,
中，是分式的个数是（ ）
A.5 B.4 C.３ D.２
2. 下列各式中，正确的是（ ）
A.
B.
C.
D.
=2
3. 下列关于分式的判断，正确的是（ ）
A.当x=2时，
的值为零 B.无论x为何值，
的值总为正数
C.无论x为何值，
不可能得整数值 D.当x
3时，
有意义
4. 把分式
中的分子分母的x、y都同时扩大为原来的2倍，那么分式的值将是原分式值的（ ）
A.2倍 B.4倍 C.一半 D.不变
5. 若方程
有增根，则增根可能为（ ）
A.0 B.2 C.0或2 D.1
6．下列函数表达式中，
均表示自变量，不是反比例函数的是（ ）
A.
B.
C.
D.
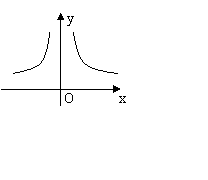
7．如图所示的图象的函数关系式只能是（ ）
A. 
B.
C. 
D.
8．已知函数
的图象经过点（2，3），下列说法正确的是（ ）
A．y随x的增大而减小 B.函数的图象只在第一象限
C．当x＜0时，必有y＜0 D.点（-2，-3）不在此函数的图象上
9．在函数(k＞0)的图象上有三点A1(x1, y1 )、A2(x2, y2)、A3(x3, y3 ),已知x1＜x2＜0＜x3,则下列各式中,正确的是 ( )
A.y1＜y2＜y3 B.y3＜y2＜y1 C. y2＜ y1＜y3 D.y3＜y1＜y2
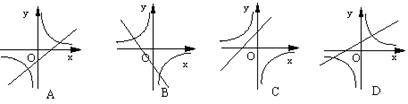
10.如图，函数y＝k（x＋k）与在同一坐标系中，图象只能是下图中的（ ）
 |
二、填空题（每小题3分，共30分）
11．不改变分式的值，使分子、分母的第一项系数都是正数，则
.
12．已知
－
＝5，则
的值是 ．
13．用科学记数法表示－0.=_____________________.
14．若分式
的值为正，则的取值范围等于_____________.
15．点（
，5）在反比例函数
的图象上，则
=________，该反比例函数的图象位于第__________象限，在每个象限内
随的增大而____________.
16．已知点A（
,
）在第二象限，且m为整数，则过A的反比例函数的关系式为__________________.
17．某食用油生产厂要制造一种容积为5升（1升＝1分米3）的圆柱形油桶，油桶的底面面积s（米2）与桶高h（米）的函数关系式为 _______ .
18. 点P在函数
的图象上，A在X轴的正半轴上，O为坐标原点，PA=PO，∠APO=Rt∠，则△POA的面积=_____________________.
19．正比例函数
的图象与反比例函数
的图象的一个交点是A，点A的横坐标是2，则此反比例函数的关系式为_________________.
20．已知直线
交轴于点A，交轴于点B，交双曲线
于点D，DC⊥轴，垂足为C，且
，则=_______________.
三、解答题（共60分）
21．（每小题4分，共16分）化简下列各式：
（1）
＋
．
（2）
.
（3）
. （4）
22．（每小题4分，共8分）解下列方程：
（1）
＋
＝3．
（2）
.
23．（6分）比邻而居的蜗牛神和蚂蚁王相约，第二天上午8时结伴出发，到相距16米的银杏树下参加探讨环境保护问题的微型动物首脑会议．蜗牛神想到“笨鸟先飞”的古训，于是给蚂蚁王留下一纸便条后提前2小时独自先行，蚂蚁王按既定时间出发，结果它们同时到达．已知蚂蚁王的速度是蜗牛神的4倍，求它们各自的速度．
24．（10分）某空调厂的装配车间原计划用2个月时间（每月以30天计算），每天组装150台空调.（1）从组装空调开始，每天组装的台数m（单位： 台／天）与生产的时间t（单位：天）之间有怎样的函数关系？（2）由于气温提前升高、厂家决定这批空调提前十天上市，那么装配车间每天至少要组装多少空调？
25．（8分）阅读材料题
对于题目“若方程
的解是正数，求a的取值范围。”有同学作了如下解答：
解：去分母，得 
化简，得
所以 
欲使方程的解为正数，必须
，得
所以当时，方程的解是正数。
上述解法是否有误？若有错误，请指出错误原因，并写出正确解法；
若无错误，请说明每一步变形的依据。
26．（12分）如图，正方形OABC的面积为9，点O为坐标原点，点B在函数（k＞0，x＞0）的图象上，点P（m、n）是函数（k＞0，x＞0）的图象上任意一点，过点P分别作x轴、y轴的垂线，垂足分别为E、F，并设矩形OEPF和正方形OABC不重合部分的面积为S.（1）求B点坐标和k的值；（2）当S＝时，求点P的坐标；
（3）写出S关于m的函数关系式.
