八年级(上)期中考试数学试题(2)及解答

八年级(上) 期中考试数学试题(2)

考试时间：90分钟　　满分：100分

一、我来填:（每题3分，共30分）

1.的相反数是__________，倒数是__________，绝对值是_________.

2.某人乘电梯从一楼到四楼，这一运动过程叫__________.

3.在△ABC中，∠C=90°，∠A=45°，AB=6，则AC=_______，S_△ABC=_________.

4.通过估算比较大小：_________（填“＞、=、＜”）.

5.实数a、b在数轴上的位置如图，则

6.我们学过的四边形中，即是轴对称，又是中心对称的图形有________、_______、_______.

7.如图，△ABC中，AC=3，AD是BC边上的中线，AD⊥AC，AD=2，则BC=________.

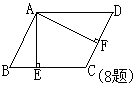
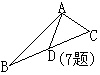
8.如图，菱形ABCD中，AE⊥BC于E，AF⊥CD于F，且E、F分别为BC、CD的中点，则∠C的度数为__________.

9.一个多边形的每个外角都等于30°，则它的边数为_________.

10.在矩形ABCD中，O为对角线AC、BD的交点，矩形ABCD的周长为34cm，△AOD与△AOB的周长差为7cm，则AC=_________.

二、我来选:（每题4分，共24分）

11.在、、π、、0、、、0.373773，这八个数中，无理数有（　）

　A.2个　　　　B.3个　　　　C.4个　　　　D.5个

12.下列说法正确的有（　）

　（1）三个角是直角的四边形是矩形；

　（2）两条对角线相等的四边形是矩形；

　（3）有两条边相等，并且另外的两条边也相等的四边形是平行四边形；

　（4）两条对角线互相垂直的矩形是正方形；

　（5）一条对角线平分一组对角的四边形是菱形.

　　A.1个　　　　B.2个　　　　C.3个　　　　D.4个

13.下列图形中，不是中心对称的图形是（　）

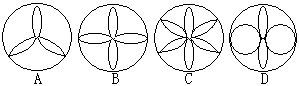
14.内角和是2160°的多边形是（　）

　A.十边形　　 B.十二边形　　C.十四边形　　D.无法确定

15.把边长分别为3cm，5cm，7cm的两个全等三角形拼成四边形一共能拼出多少个平行四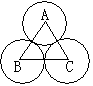边形？（　）

　A.1个　　　　B.2个　　　　 C.3个　　　　 D.4个

16.如图，三个等圆的圆心分别在正三角形ABC的三个顶点上，此图案可看做由其中一个圆，绕正三角形的中心旋转得到的其旋转角为（　）

　A.60°　　　 B.80°　　　　C.45°　　　　D.120°

三、我来探索:（第17题5分，第20、21题各6分，第22题9分，第18、19题各10分，共46分）

17.如图，∠C=90°，AC=3，BC=4，AD=12，BD=13.问AD⊥AB吗？试说明理由.

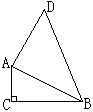
18.（1）如图，在等腰梯形ABCD中，AD∥BC，E是BC的中点，连接AE、DE，那么AE=DE吗？请说明理由.

　

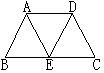
（2）上题中，若添加条件BC=2AD，图中有平行四边形吗？请说明理由.

19.计算:

（1）;（2）.

20.设，，能用含a、b的代数式表示-23吗？

21.折叠矩形纸片ABCD，先折出折痕（对角线BD，再折叠使AD与对角线BD重合，得到折痕DG.）若AB=4，AD=2，你能求出AG的长吗？

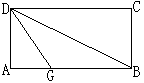
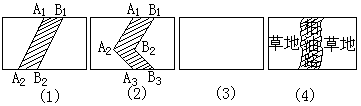
22.本题四个矩形的水平方向的边长为a，竖直方向的边长为b.在图（1）中，将线段A₁A₂向右平移1个单位到B₁B₂，得到封闭图形A₁A₂B₂B₁（即阴影部分）；在图（2）中，将折线A₁A₂A₃向右平移1个单位到B₁B₂B₃，得到封闭图形A₁A₂A₃B₃B₂B₁（阴影部分）.

（1）在图（3）中，请你类似地画一条有两个折点的折线，同样向右平移1个单位，从而得到一个封闭图形，并用斜线画出阴影；

（2）请你分别写出上述三个图形中除去阴影部分后剩余部分的面积

　　　　 S₁=_________　　S₂=_________　　S₃=__________

（3）联想与探索：如图（4），在一块矩形草地上，有一条弯曲的柏油路（路的任何地方的水平宽度都是1个单位）请你猜想空白部分表示的草地面积是多少？

答案:

一、

题号	1	2	3	4	5	6	7	8	9	10
答案		平移	9	7	-3a	正方形　菱形　矩形		120°	12	13cm

　　二、

题号	11	12	13	14	15	16
答案	B	B	A	C	C	D

三、

17.AD⊥AB.

　理由：在Rt△ACB中，∠C=90°，AC=3，BC=4，

　　　∴

　　　在△ABD中，AD=12，BD=13，AB=5，

　　　∵AB²+AD²=12²+5²=169，

　　　BD=13²=169，

　　　∴AB²+AD²=BD².

　　　∴△DAB是直角三角形.∠DAB=90°.

　　　∴AD⊥AB.

18.（1）AE=DE.

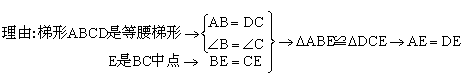
　（2）有两个平行四边形：，

　　

　　 同理：

19.（1）

　　　　　　　　

　　（2）

　　　　　　

　　　　　　

　　　　　　

20.由已知得，a²=2，b³=3.

　　　 -23=-20-3=-10a²-b³.

　　　 或-b³+a⁴，-b³+2a²等等

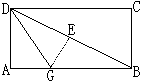21.能.

　　理由：设E为AB与BD重合时点A所在位置，则GE⊥DB，GE=AG，DE=AD.

　　　　　在Rt△DAB中，

　　　　

　　　　　设AG=x，则EG=x，DE=AD=2，BG=4-x，

　 在Rt△GEB中，GE²+BE²=GB²，即解得，即

22.（1）略，答案不唯一，只要符合要求即可

　　（2）S₁=ab-b　　S₂=ab-b　　S₃=ab-b

　　（3）草地面积为ab-b