八年级(上)数学第一次月考试卷 2005.10
一、填空题：(1至5小题每空1分，其余每空2分，共27分)
1. 64的平方根是 ；12的立方根是 ；10-6的算术平方根是 ；
(-5)0的立方根是 ；
的平方根是
。
2. 
的相反数是
；
-
的绝对值是
。
3. 比较大小：
_______ 
；
（用“>”或“<”填空）。
4. 估算：
≈
（误差小于0.1）；
≈
（误差小于1）。
5. 当x=1.44×104时，
＝_____________；若＝30，则x＝__________。
6. 大于
而小于
的整数有________________________。
7. 观察下面的等式：
=7,
=67,
=667，则
＝6667 。
8. 直角三角形中，以直角边为边长的两个正方形的面积为36
，64，则以斜边为边长的正方形的面积为__________.
9. 面积为120cm2的直角三角形，它的一条直角边为10cm，那么它的斜边长为_____cm。
10. 如图，∠OAB=∠OBC=∠OCD=90°， AB=BC=CD=1，OA=2，
则OD2=____________.
11. 小明把一根70cm长的木棒放到一个长、宽、高分别为30cm、
40cm、50cm的木箱中，他能放进去吗？答：_______________
（填“能”、或“不能”）
12. 受台风影响，马路边一棵大树在离地面6m处断裂，大树顶部落在离大树底部8m处，则大树在折断前高为 m。
13. 已知┃x－12┃＋┃z－13┃与y2－10y＋25互为相反数，则以x、y、z为三边的三角形是 三角形。
二、选择题：(每小题2分，共14分)
1. 下列说法中不正确的是 （ ）
A. －1的立方根是－1 B. 0的平方根与立方根相等
C. －4的平方根是
D. 每个数都有一个立方根
2. 下列各式中正确的是 （ ）
A. 
B. 
C. 
D. 
3．在3.141、0.33333……、
、
、
、
、0.……（相邻两个3之间0的个数逐次增加2）、0这八个数中，无理数的个数是 （ ）
A. 1个 B. 2个 C. 3个 D. 4个
4. 直角三角形两直角边长分别为6cm和8cm,则连接这两条直角边中点的线段长为（ ）
A. 10cm B. 3cm C. 4cm D. 5cm
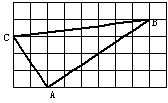
5. 如图，正方形网格中的△ABC，若小方格边长为1，则△ABC是 （ ）
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 以上答案都不对
(第5题图) (第7题图)
6. Rt△ABC的三边分别为a、b、c，则以下列长度为边的三角形是直角三角形的是（ ）
A．a＋1、b＋1、c＋1 B．ａ－１、b－1、c－1
C．2a、2b、2c C．a2、b2、c2
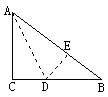
7. 如图，有一块直角三角形纸片，两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于 （ ）
A. 2㎝ B. 3㎝ C. 4㎝ D. 5㎝
三、计算题：(每小题5分，共20分)
(1) 
(2) 
(3) 
(4) 
四、解答题：(共11分)
1．(4分)人造地球卫星要绕地球旋转，必须克服地球引力，克服地球引力的速度称为逃逸速度，逃逸速度的计算公式为
（千米/秒），其中g=0.0098千米/秒2，R=6370千米，求逃逸速度。（结果保留2个有效数字）
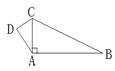
2．(7分)如图，CA⊥AB，AB=12，BC=13，DC=3，AD=4，求四边形ABCD的面积。
五、探究题：(共28分)
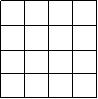1. (6分)如图，正方形网格中的每个小正方形边长都是1，任意连结这些小正方形的顶点，可得到一些线段。请在图中画出
这样的线段，并选择其中的一个说明这样画的道理。
 |
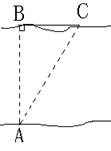2． (5分)某人欲从A点横渡一条河，由于水流的影响，实际上岸地点C偏离欲到达点B 240米，结果他在水中实际游了510米，求该河的宽度。
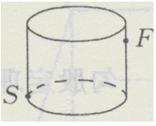3. (6分)如图所示，圆柱形玻璃容器，高18
cm，底面周长为60 cm，在外侧距下底1 cm,点S处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口外侧距开口处1 cm的点F处有一苍蝇，试求急于捕获苍蝇充饥的蜘蛛，所走的最短路线的长度．
4．(5分)用长3cm，宽2.5cm的邮票30枚不重不漏地拼成一个正方形。求：①这个正方形的边长是多少？②请你设计出拼图方案。
5. (6分)观察下面式子，根据你得到的规律回答：
=____；
=____；
=____；……
求
的值(要有过程)。