期中综合测试
（时间：120分钟 总分：120分）
一、选择题（每小题3分，共30分）
1．下列各式：
其中分式共有（ ）个。
A、2 B、3 C、4 D、5
2. 下列函数中，是反比例函数的是（ ）
A. 
B.
C. 
D.
3. 下列关于分式的判断，正确的是（ ）
A.当x=2时，
的值为零 B.无论x为何值，
的值总为正数
C.无论x为何值，
不可能得整数值 D.当x
3时，
有意义
4. 下列各式正确的是（ ）
A、
B、
C、
D、
5. 下列说法正确的是（ ）
A.若 a、b、c是△ABC的三边，则a2＋b2＝c2
B.若 a、b、c是Rt△ABC的三边，则a2＋b2＝c2
C.若 a、b、c是Rt△ABC的三边，
，则a2＋b2＝c2
D.若 a、b、c是Rt△ABC的三边，
，则a2＋b2＝c2
6．已知一个直角三角形的两边长分别为3和4，则第三边长是（ ）
A．5 B．25 C．
D．5或
7．直角三角形有一条直角边为6，另两条边长是连续偶数，则该三角形周长为（ ）
A. 20 B. 22 C. 24 D. 26
8．如果反比例函数
的图象经过点（－3，－4），那么函数的图象应在（）
A、 第一、三象限 B、第一、二象限 C、第二、四象限 D、第三、四象限
9．函数
与
（
）的图象的交点个数是（ ）
A. 0 B. 1 C. 2 D. 不确定
 |
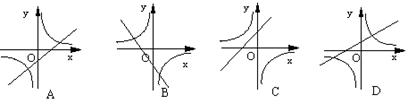10. 在同一坐标系中，函数
和
的图象大致是 （ ）
A B C D
二、填空题（每小题2分，共20分）
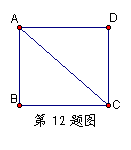11化简：
=________； 
=___________.
12．在△ABC中，∠C=90°， AB＝5，则
+
+
=_______．
.
13．已知
－
＝5，则
的值是 ．
14．正方形的对角线为4，则它的边长AB= .
15．如果梯子的底端离建筑物9米，那么15米长的梯子可以到达建筑物的高度是______米.
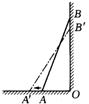
16．如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为2米，梯子的顶端B到地面的距离为7米．现将梯子的底端A向外移动到A’，使梯子的底端A’到墙根O的距离等于3米，同时梯子的顶端
B下降至 B’，那么 BB’的值： ①等于1米；②大于1米5；③小于1米.其中正确结论的序号是 ．
17．如图，是2002年8月北京第24届国际数学家
大会会标，由4个全等的直角三角形拼合而成.如果
图中大、小正方形的面积分别为52和4，那么一个
直角三角形的两直角边的和等于 ．
|
|
18．某食用油生产厂要制造一种容积为5升（1升＝1立方分米）的圆柱形油桶，油桶的底面面积s与桶高h的函数关系式为 .
19．若函数
与
的图象有一个交点是（
，2），则另一个交点坐标是_________。
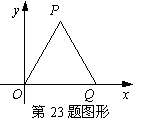20．如右图，△OPQ是边长为2的等边三角形，
若反比例函数的图象过点P，则它的解析式是_______。
三、解答题（共70分）
21．（每小题4分，共16分）化简下列各式：
（1）．
（2）
.
（3）. 
（4）
22．（每小题4分，共8分）解下列方程：
（1） 
（2）
+
23．（6分）某校八年级学生到离校15千米的山坡植树，一部分学生骑自行车，先出发
小时，其余学生乘汽车出发，结果同时到达，汽车速度是自行车速度的3倍，求自行车、汽车的速度各是多少？
24．（6分）印度数学家什迦逻（1141年-1225年）曾提出过“荷花问题”：
“平平湖水清可鉴，面上半尺生红莲；
出泥不染亭亭立，忽被强风吹一边，
渔人观看忙向前，花离原位二尺远；
能算诸君请解题，湖水如何知深浅？”
请用学过的数学知识回答这个问题.
`
25．（8分））如图，有一个直角三角形纸片，两直角边AC=6cm,BC=8cm,现将直角边AC沿
∠CAB的角平分线AD折叠，使它落在斜边AB上，且与AE重合，你能求出CD的长吗？
 |
26．（8分）某空调厂的装配车间原计划用2个月时间（每月以30天计算），每天组装150台空调.
（1）从组装空调开始，每天组装的台数m（单位： 台／天）与生产的时间t（单位：
天）之间有怎样的函数关系？
（2）由于气温提前升高、厂家决定这批空调提前十天上市，那么装配车间每天至少要组装多少空调？
27．（8分）某商场出售一批名牌衬衣，衬衣进价为80元，在营销中发现，该衬衣的日销售量y（件）是日销售价x（元）的反比例函数，且当售价定为100元/件时，每日可售出30件。
（1）请求出y与x之间的函数关系式。
（2）若商场计划经营此种衬衣的日销售利润为2000元，则其单价应定为多少元？
28．（10分）10、如图，正方形OABC的面积为9，点O为坐标原点，点B在函数y=
(k>0,x>0)的图象上，点P（m, n）是函数y= (k>0,x>0)的图象上任意一点，过点P分别作x轴、y轴的垂线，垂足分别为E、F，并设矩形OEPF和正方形OABC不重合部分的面积为S。（提示：考虑点P在点B的左侧或右侧两种情况）
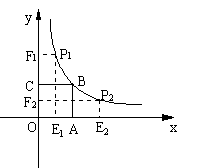（1）求B点坐标和k的值；
（2）当S= 
时，求点P的坐标；
（3）写出S与m的函数关系式。