初二年数学(下)期中检测试卷
（考试时间：120分钟 满分：100分）
|
| 一 | 二 | 三 | 四 | 总 | ||||||||
| 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 分 | |||
| 得分 | |||||||||||||
题序一、选择题（15×2分）
1、2的平方根是……………………………………………………..（ D ）
A、4
B、±4 C、
D、±
2、在实数
、
、0、
、
、
、
、
、2.……中，无理数的个数为…………………………（ C ）
A、2个 B、3个 C、4个 D、5个
3、下列说法正确的是……………………………………………….（ B ）
A、
的立方根为
B、9的平方根为
C、—27没有立方根 D、1的平方根是它本身
4、在下列各组根式中，是同类二次根式的为…………………….（ B ）
A、与
B、
与
C、与
D、与
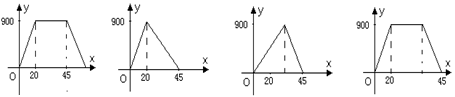
5、小明的父亲饭后散步，从家中走20分钟到一个离家900米的报亭看10分钟的报纸后，用15分钟返回家中，下列图形中表示小明父亲离家的时间与距离之间的关系是……………………………………………….（ D ）
A
B
C
D
6、下列各组线段中，成比例的是………………………..（B ）
A、1，2，3，4 B、1，2，3，6
C、1，3，2，5 D、2，3，4，5
7、下列计算中，正确的是……………………………….（ D ）
A、+=
B、
=5
C、
=
D、
8、函数y=
中，自变量x的取值范围是…………(
C )
A、x＞-
B、x＜- C、x≠- D、x≠0
9、点P（1，-2）关于x轴的对称点坐标为……………（ A ）
A、（1，2） B、（-1，2） C、（-1，-2） D、（2，1）
10、若M＜0，N＞-2，则点（M，N+2）在………………（ C ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
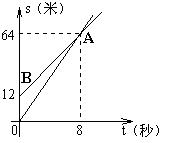11、如图，OA，BA分别表示甲、乙两名
学生运动的一次函数图象，图中s和t分
别表示运动路程和时间，根据图象判断快
者的速度比慢者的速度每秒快（ C ）
A、2.5米 B、2米
C、1.5米 D、1米
12、与数轴上的点一一对应的数是（ D ）
A、分数或整数 B、无理数 C、有理数 D、有理数或无理数
13、一次函数y=x图象向下平移2个单位长度后，对应的函数关系式是
………………………………………………………………………...（D ）
A、y=2x B、y=x C、y=x +2 D、y=x－2
14、已知正比例函数
（
）的函数值
随
的增大而减小，则一次函数
的图象大致是…………………………….（ B ）．
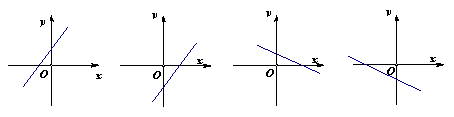
A、 B、 C、 D、
15、一次函数
，经过（1，1），（2，－4），则
与
的值为（ C ）．
A、
B、
C、
D、
二、填空题：（每空2分，共18分）
16、
的绝对值＝
，
＝－4， 
＝－1；
17、若3x－5y=0，则
＝
。
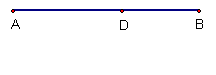18、如图，D是AB上的一点，且AD：DB＝3：2，则DB：AB的值为2 ：5
第3题图
19、点P（3，-5）到X轴的距离为5个单位长度。
20、写一个不经过第一象限的一次函数解析式y ＝－x－4。
21、点B（0，－4）在直线
图象上，则＝－4
22、我国是一个严重缺水的国家，大家都应倍加珍惜水资源，节约用水。据测试，拧不紧的水龙头每秒钟滴下2滴水，每滴水约0.05毫升，小明同学洗手时，没有把水龙头拧紧，当小明离开x小时后，水龙头滴y毫升的水，试写出y关于x的函数关系式
y ＝360x (x≥0).
三、化简或计算（共8×5分）：
23、计算：
24、计算：(3＋)2
25、
；
26、
27、
28、
29、
30、
四、解答题：（每小题6分，共12分）
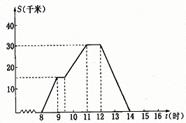31、一天上午8时，小华去县城购物，到下午2时返回家，结合图像回答：
（1） 小华何时第一次休息？
（2） 小华离家最远的距离时多少？
（3） 返回时平均速度时多少？
（4） 请你描述一下小华购物的情况。
32．一次函数y=kx+b交x轴于点A（3，0），交y轴于点B（0，2）。
（1）画出这个函数的图象
（2）求这个函数的解析式
（3）求这个图象与坐标轴围成的三角形面积。