八年级数学第十七章测试题
一、填空题
1.已知点M(a-3,a+2)在y轴上,则a= 。
![]() 2.点P(-6,4)到x轴的距离为 ,到y轴的距离为 。
2.点P(-6,4)到x轴的距离为 ,到y轴的距离为 。
3.函数中的自变量x 的取值范围是 。
4.函数![]() 的图象与y轴的交点是
,与x轴的交点是 。
的图象与y轴的交点是
,与x轴的交点是 。
5.若反比例函数![]() 的图象经过点(3,-4),则此函数的解析式为 。
的图象经过点(3,-4),则此函数的解析式为 。
6.若点P(a,b)在第四象限,则点(b,-a)在第 象限.
7.一次函数y=kx+b中,y随x的增大而减小,且kb>0,则这个函数的图象一定经过第 象限。
8.写出一个y随x的增大而减小的正比例函数的表达式 。
9.A、B两地之间的距离是160千米,若汽车以平均每小时80千米的速度从A地开往B地,则汽车距B地的路程y(千米)与行驶时间x(小时)之间的函数关系式为 。
10.近视眼镜的度数y(度)与镜片的焦距x(米)成反比例,已知400度近视眼镜片的焦距为0.25米,则眼睛度数为y(度)与镜片焦距x之间的函数关系式为 。
|
|
|
|
|
|
![]()
![]() 13.当自变量x由小到大时,函数y的值反而减少的是( )
13.当自变量x由小到大时,函数y的值反而减少的是( )
A B y=2x C D y=-2+5x
![]()
![]()
![]()
![]() 14.经过点(2,-3)的双曲线是 ( )
14.经过点(2,-3)的双曲线是 ( )
A B C D
15.2004年6月3日中央新闻报道,为鼓励居民节约用水,北京将出台新的居民用水收费标准:①若每月每户居民用水不超过4立方米,则按每立方米2元计算;②若每月每户居民用水超过4立方米,则超过部分按每立方米4.5元计算(不超过部分仍按每立方米2元计算).现假设该市某居民某月用水x立方米,水费为y元,则y与x的函数关系用图表![]()
![]()
![]()
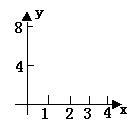
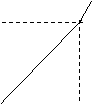
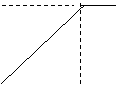


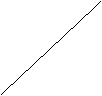
![]()
![]() 示正确的是( )
示正确的是( )

A B C D
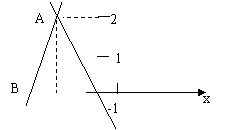
![]() 16.已知一次函数y=kx+b的图象如图,当x<0时,y的取值范围是 ( )
16.已知一次函数y=kx+b的图象如图,当x<0时,y的取值范围是 ( )
|
 A y >0 B y<0
A y >0 B y<0
![]() C -2<y<0 D y<-2
C -2<y<0 D y<-2
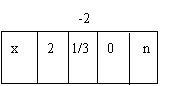 |
|
|
|
|
|
C m=3 n= -![]() D m= -3 n= -
D m= -3 n= -![]()
18.一条直线平行于直线y=2x-1,且与两坐标轴围成的三角形面积是4,则这条直线的解析式是 ( )
A y=2x+4 B y=2x-4 C y= 2x±4 D y=x+2
19.函数y= -x-1的图象不可能经过( )
A 第一象限期 B 第二象限 C 第三象限 D第四象限
20.无论m为何实数,直线y=x+2m与y= -x+4的交点不可能在( )
![]() A 第一象限 B 第二象限 C 第三象限
D 第四象限
A 第一象限 B 第二象限 C 第三象限
D 第四象限
|
|
|
|
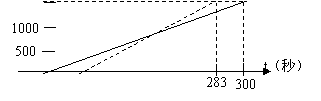 |
(图中实线为甲的路程与时间的关系图象,虚线为乙的路程与时间的关系图象)小王根据图象得到如下四个信息,其中错误的是( )
A 这是一次1500米的赛跑 B 甲、乙两人中乙先到达终点
C 甲、乙同时起跑 D 甲的这次赛跑中的速度为5米/秒
三解答题
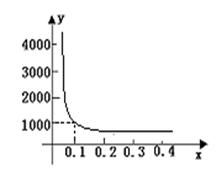 22.在压力不变的情况下,某物体承受的压强P是它的受力面积S的反比例函数,其图象如图所示:
22.在压力不变的情况下,某物体承受的压强P是它的受力面积S的反比例函数,其图象如图所示:
(1) 求P与S之间的关系式;
(2) 求当S=0.5时物体承受的压强P
23.已知一次函数y=kx+b,当x=-4时,y的值为9,当x=2时,y的值为-3。
(1) 求这个函数的解析式;
(2) 在直角坐标系中画出这个函数的图象。
|
 |
![]()
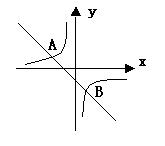
![]() 25.如图,一次函数y=kx+b的图象和反比例函数
25.如图,一次函数y=kx+b的图象和反比例函数![]() 的图象交于A、B两点:A(-2,1),B(1,n)
的图象交于A、B两点:A(-2,1),B(1,n)
(1) 求反比例函数的关系和一次函数关系的解析式;
(2) 根据图象写出使一次函数的值大于反比例函数
值的x的取值范围。
26.作出函数y=2x-4的图象,并根据图象回答下列问题:
(1) 当 -2≤x≤4时,求函数y的取值范围;
(2) 当x取什么值时,y<0,y=0,y>0?
(3) 当x取何值时,-4<y<2?
27某影碟出租店要设两种租碟方式:一种是零星租碟,每张收费1元;另一种是会员卡租碟,办卡费每月12元,租碟费每张0.4元,小彬常来租碟,若每月租碟数量为x张,
(1) 写出零星租碟方式应付金额y1(元)与租碟数量x(张)之间函数关系式;
(2) 写出会员卡租碟方式应付金额y2(元)与租碟数量x(张)之间的函数关系式;
(3) 小彬选取哪种方式更合算?
参考答案
一、1.3 2. 4,6 3. x>1/2 4.(0,-7),(27,0) 5. y= -12/x
6. 三, 7. 二、三、四 8. y= -2x等 9. y=160-80x 10. y=100/x 11.(9,12)
二、12.D 13.C 14. A 15. C 16. D 17. C 18. C 19. A 20. C 21.C
三、22 (1)P=100/s (2)当s=0.5 时,P=200 23. (1)y=-2x+1, (2) 略 24. l1:y= -2x
l2:y=3x+5 25.(1)y= -2/x,y= -x-1 (2)x<-2或0<x<1 26. (1) -8≤y≤4 (2)x<2, x=2, x>2 (3) 0 <x<3 27. (1) y1=x, (2) y2=0.4x+12 (3) 当x>20时,应选会员卡方式;当x=20时,两种方式一样;当x<20时,选零星租碟方式.