赵家中学初中2007级期中统一考试数学试卷
本试卷分第I卷 和第Ⅱ卷 两部分，共三大题，满分150分，考试时间120分钟
第I卷 （选择题 共48分）
一、选择题：（本大题12个小题，每小题4分，共48分）每小题只有一个答案是正确的，
1．若 ，则的值是……………………………………………………( )
A. B. C. D.
2． 计算
的结果是…………………………………………………（ ）
A． 
B．
C． 
D．.
3．不等式组
的正整数解的个数是……………………………………（ ）
A．1个 B．2个 C．3个 D．4个
4．如果代数式
有意义，那么
的取值范围是……………………………（ ）
A．
B．
C．
D．
5．下列分解因式中，最后结果正确的是………………………………………（ ）
A．
B．
C．
D．
6．某校学生暑假乘汽车到外地参加夏令营活动，目的地距学校120km。一部分学生乘慢车先行,出发1h后，另一部分学生乘快车前往，结果他们同时到达目的地。已知快车速度是慢车速度的1.5倍,如果设慢车的速度为
,那么可列方程为……………………………………………………………………………（ ）
A.
－
B.－
C.
D.
7．若方程
有增根，则它的增根是……………………（ ）．
A．0 B．1 C．－1 D．1和－1
8．平面直角坐标系中的点P
关于轴的对称点在第四象限，则
的取值范围在数轴上可表示为………………………………………………………………（ ）
9．如图，小亮拿一张矩形纸图（1），沿虚线对折一次得图（2），下将对角两顶点重合折叠得图（3）。按图（4）沿折痕中点与重合顶点的连线剪开，得到三个图形，这三个图形分别是………………………………………………………………………（ ）
A．都是等腰梯形 B．都是等边三角形
C．两个直角三角形，一个等腰三角形 D．两个直角三角形，一个等腰梯形
10．如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是……………………………………………………………………………………( )
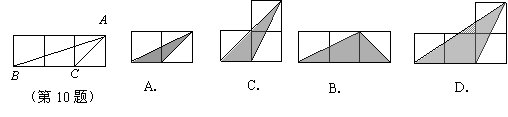
11．已知
,直线
一定经过的象限是…………(
)
A．第一、二、三象限 B．第二、三、四象限
C．第二、三象限 D．第三、四象限
12．同学们还记得“乌鸦喝水”的故事吧，在一片树林里有一只丢弃的圆柱体玻璃瓶中盛了一点水，由于瓶口直径D
较小，水又比较少，只有h高，而瓶高有H （H>h）乌鸦根本喝不到水，那么乌鸦需叨（ ）
的碎石子才能喝到水（与瓶口持平）又不至于溢出来。…………………………………………………………………( )
A.
B.
C.
D.
第Ⅱ卷 （非选择题 共102分）
二、填空题：（本大题12个小题，每小题3分，共36分）请将答案直接填写在横线上
13．分解因式：
＝
。
14．方程
的解是
。
15．如果 
，那么
。
16．不等式组
的解是
，则
的取值范围是 。
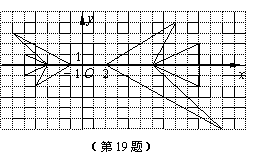
17．如图，在△ABC中，DE∥BC，若
，DE＝2，则BC的长为 。
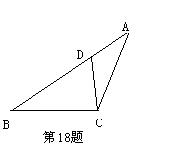
18．如图，D是△ABC的边AB上的点，请你添加一个条件，使△ADE与△ABC相似．你添加的条件是 。
19．某学习小组在讨论 “变化的鱼”时，知道大鱼与小鱼是相似图形（如图）．则小鱼上的点（a，b）对应大鱼上的点的坐标为 。
20．如图，已知线段AB，点C在AB上，且有
，则
的数值为
；
若AB的长度与中央电视台演播厅舞台的宽度一
样长，那么节目主持人应站在 位置最好。
21.已知
与
互为相反数,则式子
的值为
。
22．期中考试后，学习小组长算出全组 5位同学数学成绩的平均分为M，如果把M当成另一个同学的分数，与原来的5个分数一起，算出这6个分数的平均值为N，那么M：N为 。
23．在一次主题为“学会生存”的中学生社会实践活动中，春华同学为了锻炼自己，他通过了解市场行情，以每件6元的价格从批发市场购进若干件印有2008北京奥运标志的文化衫到自由市场去推销，当销售完30件之后，销售金额达到300元，余下的每件降价2元，很快推销完毕，此时销售金额达到380元，春华同学在这次活动中获得纯收入＿ 元。
24．若关于的方程
的根大于0,则的取值范围是
。
三、解答题：（本大题8个小题，共66分）下列各题解答时必须给出必要的演算过程或推理步骤。
25．（本题满分 8分）分解因式
(1).
(2).
26．（本题满分 8分）已知关于
的方程组
的解满足
，求的取值范围．
27．（本题满分7分）化简：
，然后请自选一个你喜欢的值，再求原式的值.
28．（本题满分 7分）解方程： 
（温馨提示：这是分式方程，别忘了验根哦。）
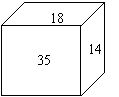29．（本题满分 8分）.如图，立方体的每一个面上都写有一个自然数，且相对两面所写的两数之和都相等。若18对面写的是质数，14对面写的是质数
，35对面写的是质数
，试求代数式
的值。
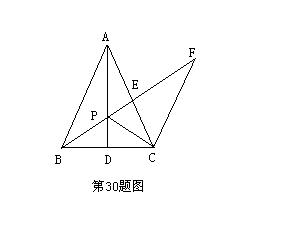30. （本题满分 8分）如图DABC中，AB=AC，AD是中线，P是AD上的一点，过点C作AB的平行线CF，延长 BP交AC与E，交CF 与F.试说明DEPC∽DCPF
31. （本题满分 10分）某公司为了扩大经营，决定购进6台机器用于生产某种活塞。现有甲、乙两种机器供选择，其中每种机器的价格和每台机器日生产活塞的数量如下表所示。经过预算，本次购买机器所耗资金不能超过34万元。
| 甲 | 乙 | |
| 价格（万元/台） | 7 | 5 |
| 每台日产量（个） | 100 | 60 |
（1）按该公司要求可以有几种购买方案？
（2）若该公司购进的6台机器的日生产能力不能低于380个，那么为了节约资金应选择哪种方案？
32．（本题满分 10分） 某高速公路收费站，有m（m>0）辆汽车排队等候收费通过。假设通过收费站的车流量（每分钟通过的汽车数量）保持不变，每个收费窗口的收费检票的速度也是不变的。若开放一个收费窗口，则需20分钟才可能将原来排队等候的汽车以及后来接上来的汽车全部收费通过；若同时开放两个收费窗口，则只需8分钟也可将原来排队等候的汽车以及后来接上来的汽车全部收费通过。若要求在3分钟内将排队等候收费的汽车全部通过，并使后来到站的汽车也随到随时收费通过，请问至少要同时开放几个收费窗口？
赵家中学初中2007级期中统一考试数学试卷
参考答案
一、选择题：（本大题12个小题，每小题4分，共48分）每小题只有一个答案是正确的，
1.A 2.D 3.C 4.D 5.D 6.A 7.B 8.B 9.C 10.A 11.C 12.B
二、填空题：（本大题12个小题，每小题3分，共36分）请将答案直接填写在横线上
13.
14.
15.
16.
17.
18.∠ACD=∠ABC 或∠ADC=∠ACB 或
19. 
20
C
21.
22.1 23.140元 24
三、解答题：（本大题8个小题，共66分）下列各题解答时必须给出必要的演算过程或推理步骤。
25．（本题满分 8分）分解因式
(1).
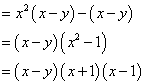
(2).
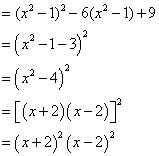
26.
27解：原式
……………………（3分）
…………………………………………….（5分）
…………………………………………….（6分）
……………………………………………（7分）
28.方程两边同乘以（X+1）（X-1）…………………………………………….2分
2 -(
-1)=-X(X-1)………………………………………4分
X=3…………………………………………………………6分
经检验:X=3是原方程的根……………………………….7分
∴ X= 3………………………………………………
29.解根据题意得,18+a=14+b=35+c.
所以,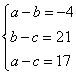
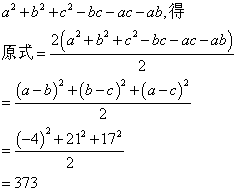
30.
３1、（1）设购买甲种机器x台，则购买乙种机器（6－x）台。
由题意，得
，
解这个不等式，得
，即x可以取0、1、2三个值，
所以，该公司按要求可以有以下三种购买方案：
方案一：不购买甲种机器，购买乙种机器6台；
方案二：购买甲种机器1台，购买乙种机器5台；
方案三：购买甲种机器2台，购买乙种机器4台；
（2）按方案一购买机器，所耗资金为30万元，新购买机器日生产量为360个；按方案二购买机器，所耗资金为1×7＋5×5＝32万元；，新购买机器日生产量为1×100＋5×60＝400个；按方案三购买机器，所耗资金为2×7＋4×5＝34万元；新购买机器日生产量为2×100＋4×60＝440个。因此，选择方案二既能达到生产能力不低于380个的要求，又比方案三节约2万元资金，故应选择方案二。
32 解:设每个收费窗口每分钟可收费通过 x辆汽车,每分钟的车流量为y辆,又设需要开放n个收费窗口,才能在3分钟内将排队等候的汽车全部收费通过,根据题意得.
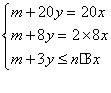解之得,