-重庆一中初2007级下期数学半期试题 2006.4
（考试时间：120分钟 满分：150分）
一 选择题.（每小题4分，共40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1 在
、
、
、
、
、
中分式的个数有（
）。
A 2个 B 3个 C 4个 D 5个
2 下列从左到右的变形是因式分解的是（ ）。
A（ a+3）(a-3)=a2 –9 B. x2+x-5=x(x+5)-5
C x2+1=x(x+.) D x2+4x+4=(x+2)2
3 一元一次不等式组 
解集在数轴上表示正确的是（
）。
|
|
|
|
 | |||
| |||
|
|
|
|
4下列两个图形必定相似的是（ ）。
A 有两条边对应成比例的等腰三角形；
B 有一个角是25度的等腰三角形；
C 有一个角是100度的等腰三角形；
D 有一个角相等，两边对应成比例的三角形；
5 如果把分式
中的 x,y都扩大7倍，那么分式的值（ ）。
A. 扩大7倍 B 扩大14倍 C 扩大21倍 D 不变
6 在有理数范围内，下列各多项式能用公式法进行因式分解的是（ ）。
A.a2-6a B.a2-ab+b2 C.a2-ab+
b2 D.
a2-ab+b2
7：设“●”、“▲”、“■”表示三种不同的物体，现用天平称两次，情况如图所示，那么“●”、“▲”、“■”这三种物体质量从大到小的顺序正确的是（ ）。
A ■、●、▲ B ■、▲、●
C ▲、●、■ D ▲、■、●
 | |||
 | |||
8 应中共中央总书记胡锦涛的邀请，中国国民党主席连战先生、亲民党主席宋楚渝先生分别从台湾来大陆参观访问，先后来到西安，都参观了新建成的“大唐芙蓉园”，该园占地面积约为800000m2，若按比例尺1:2000缩小后，其面积大约相当于（ ）
A 一个篮球场的面积； B 一张乒乓球台台面的面积；
C 《重庆时报》的一个版面的面积； D 数学课本封面的面积。
9若方程 
有增根，则它的增根是（ ）
A 0 B -1 C 1 D 1和-1
10 已知
则直线y=kx+2k一定经过（ ）
A 第一，二象限； B 第二，三象限；
C 第三，四象限； D 第一，四象限；
二、
填空题（每小题4分，共40分）
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 |
11 用不等式表示“x的5倍是非负数”得： 。
12 若分式
的值为零，则x=
。
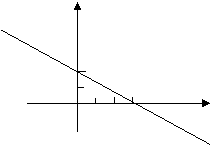
13 一次函数
的图像如图所示，当x
时，y>2。
|
DB，DE＝3，求BC＝
。
 |
|
|
|
 | |||||||
| |||||||
| |||||||
| |||||||
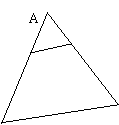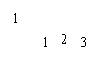(第14题) (第13题)
15 若
是一个完全平方式，则k＝
。
16 登山前，登山者要将矿泉水分装在旅行包内带上山，若每人2瓶，则剩余3瓶；若每人带3瓶，则有一人所带矿泉水不足2瓶。则登山有 人。
17 已知正方形的面积是
，利用分解因式写出表示该正方形的边长的代数式
。
18 如图，乐器上的一根弦AB＝80cm，两个端点A、B固定在乐器板面上，支撑点C是靠近点B的黄金分割点（即AC是AB与BC的比例中项），支撑点D是靠近点A的黄金分割点，则AC＝ cm；DC＝ cm。
19 一项工程，A单独做m小时完成。A，B合作20小时完成，则B单独做
需 小时完成。
20已知：
，则A＝ ；B＝
。
 |
三．解答题
21（10分，每小题5分）
（1）分解因式：9(m＋n)²-(m-n)² （2）解不等式组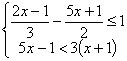
22解方程（5分）
；
23 先化简，再选择你喜欢的数代入求值（8分）
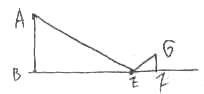
24（8分）为了测量学校一棵参天古树的高度，我校数学兴趣小组做了如下探索：
实践1：利用一根标竿和一根皮尺设计出如图1的测量方案，把长为2.5米的标竿竖直插入离树（AB）8.7米的点E处，然后沿着直线BE后退到点D，这时眼睛恰好通过标竿顶点F，看到树的顶点A。再用皮尺测得DE＝2.7米。观察者目高CD＝1.6米。他们利用相似原理求得树高为5.4米。
实践2：提供选用的测量工具有①皮尺一根、②教学用三角板一副、③镜子一面、④测角仪一个。请你设计测量方案，并根据你所设计的测量方案回答下列问题。
（1） 在你设计的方案中，选用的测量工具是（用工具的序号填写） 。
（2） 在图2中画出你测量方案的示意图。
（3） 你需要测得示意图中哪些数据。并分别用a、b、c等表示测得数据 。
（4） 写出求树高（AB）的等式，AB＝ 。（用a、b、c等字母表示）
25.（10分） 仔细阅读《战鸽总动员》中的对话，并回答问题。
根据对话内容判断，小B超过最高时速了吗？为什么？
 |
26（8分） 有一客轮往返于重庆和武汉之间，第一次做往返航行时，长江的水流速度为a千米/小时；第二次做往返航行时，正遇上长江发大水，水流速度为b千米/小时（b>a）。已知该船在两次航行中，静水速度都为V千米/小时，问该船两次往返航行所花时间是否相等，若你认为相等，请说明理由；若你认为不相等，请分别表示出两次航行所花的时间，并指出哪次时间更短些？
27.（11分） “五一”将至，某商场计划进A、B两种型号的衬衣共80件，商场用于买衬衣的资金不少于4288元，但不超过4300元。两种型号的衬衣进价和售价如下表：
| A | B | |
| 进价（元/件） | 50 | 56 |
| 售价（元/件） | 60 | 68 |
（1） 该商场对这种型号的衬衣有哪几种进货方案。
（2） 该商场如何获得利润最大。
（3） 现据商场测算，每件B型衬衣的售价不会改变，每件A型衬衣的售价将会提高m元（m>0），且所有的衬衣可全部售出，该商场又将如何进货才能满足获得利润最大。（注：利润＝售价－成本）
28（10分）如图，在△ABC中，∠B=90°，AB=6㎝，BC=8㎝。点P从A开始沿AB边向点B以1㎝∕s的速度移动，点Q从点B开始沿BC边向点C以2㎝∕s的速度移动。若P、Q分别从A、B同时出发，
（1） 
如图（1），经过多少时间，△PBQ与△ABC相似？
|
|
|
|
|
|
|
|
|
|
|
|
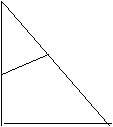（2） 如图（2），当P到B后又继续在BC上前进，Q到C后又继续在CA上前进，经过多少时间，可以使得△CPQ的面积为12.6㎝2？
命题人：邱秦飞
审题人：付 黎
重庆一中初2007级下期数学半期试题 2006.4
一. 选择题.（每小题4分，共40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | D | C | C | D | C | B | C | C | B |
二. 填空题（每小题4分，共40分）
11.
12.
13.
14.
15.
16.5 17.
18.
19.
20.1, 2
三．解答题
21（10分，每小题5分）
（1）分解因式：9(m＋n)²-(m-n)²
解:原式
(4分)
(5分)
（2）解不等式组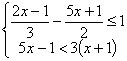
解:由①得:
(2分)
由②得:
(4分)
∴原不等组的解集为:
(5分)
22解方程（5分）；
解:
∴
(4分)
经检验是原方程的解.(5分)
23.
解:原式
(6分)
(注:
取不为2, -3, 0的任意实数均可,如:当
1时,原式
) (8分)
24.(1) ①③
(2)
(3) 
(4)
(注:此题答案不唯一)
25.解:设小V的平均速度为
,则小B的平均速度为
(1分)
由题意得:
(4分)
解得:
经检验是原方程的解且符合题意. (6分)
∴
∵
(9分)
答:小B未超过最高时速. (10分)
26.设两次航行的路程都为S. (1分)
第一次所用时间为:
(3分)
第二次所用时间为:
(5分)
∵
∴
∴
∴
∴第一次的时间要短些. (8分)
27.解:(1)设A型衬衣进件,B型衬衣进
件,则:
(1分)
(2分)
解得:
∵为整数
∴为30, 31, 32
∴有3种进货方案: A型30件,B型50件
A型31件,B型49件
A型32件,B型48件 (4分)
(2)设该商场获得利润为
元.
∵
∴随增大而减小.
∴当
时
=900
即A型30件,B型50件时获得利润最大. (7分)
(3)由题意可知
(8分)
①
时,随增大而减小,当即A型30套,B型50套时利润最大.
②
时,三种进货方式利润一样大.
③
时,随的增大而增大.当
即A型32套.B型48套时利润最大.(11分)
28.解:(1)设经过秒,△PBQ与△ABC相似,则AP=, BP=
,BQ=
(1分)
①若△PBQ∽△ABC 
即
∴
(S)
(3分)
②若△PBQ∽△CBA 
即
∴
(S)
∴经过
时,△PBQ与△ABC相似. (5分)
(2)过Q作QD⊥BC于D点.
在△CDQ与△CBA中
∴△CDQ∽△CBA
∴
设经过
秒∴
∴
∴
(7分)
在△CPQ中,QD⊥CP
∴
(8分)
当
时 解得
.
当
时,即经过7秒,P在BC上距点C7m处,Q在AC上距点C6m处.符合题意.
当
时,即经过11秒,P在BC上距点C3m处,而Q在AC上距点C14m处,不合题意,故舍去.
∴当经过7秒时,可以使△CPQ的面积为12.6cm2.