浙教版八年级数学（下）测试卷
1．下列各式中，不是二次根式的是（ ）
A．
B．
C．
D．
2.下列运算正确的是 （ ）
A．
B．
C．-3
+=-2
D．
3、如果
是二次根式，那么
应适合的条件是（ ）
A、≥3 B、≤3 C、＞3 D、＜3
4.一个容量为80的样本最大值为140,最小值为50,取组距为10,则可以分成( ).
A. 10组 B. 9组 C. 8组 D. 7组
5. 在样本的频数分布直方图中,有9个小长方形,若中间一个长方形的面积等于其他8个小长方形面积的和的三分之一,且样本数据有100个,则中间一组的频数为______
6、(1)
=______(2) 
=______（3）
=______(4)当
时，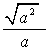
的值是 ．（5）
中x的取值范围是___________（6）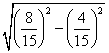
=________
7.用反证法证明命题:对于任何实数a,都有a2≥0,应假设_____________
8.在等边ΔABC中,AB=AC=BC=2
,则BC边上的高是____________
9．已知RtΔABC，∠C＝Rt∠，BC＝，AC＝
，则斜边长 斜边上的高长 。
10．在一坡比为1:7的斜坡上种有两棵小树，它们之间的距离（AB） B
为10米，则这两棵树的高度差（BC）为 米． C A
11.某种童鞋原价为100元，由于店面转让要清仓，现连续两次降价处理，现以64元销售，已知两次降价的百分率相同，每次降价的百分率为x,,则可列方程为___________________
12.某市2006年的社会总产值比2004年增长21﹪,若平均每年增长的百分率为x,可列方程:______________
13、一元二次方程 有实数根，则k的取值范围是
一次会议上,每两个都相互握了一次手,一共握了78次,若参加会议的人数是x人,则可列方程为:__________
14命题“全等三角形的对应边上的角平分线相等”中，题设是_____________________结论是_______________ 命题“同位角相等，两直线平行”写成“如果。。。。。。那么。。。。。。”的形式是：_______________________________
15．用反证法证明(填空)：在三角形的内角中，至少有一个角大于或等于60°
已知：如图∠A, ∠B,∠C是三角形ABC的内角
求证：∠A, ∠B,∠C中至少有一个角大于或等于60°
证明：假设所求证的结论不成立，即∠A__60°, ∠B___60°,∠C___60°
则∠A+∠B+∠C___180°,这与________________________矛盾
所以_________不成立,所求证的结论成立.
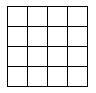
16、在如图的4×4的方格内画△ABC，使它的顶点都在格点上，三条边长分别为1，
，
。
17计算(1) 
(3)已知
(2) 
18解下列方程(1)y2-2y+1=0
(2) 4x -x2-1=0(用配方法)
(3) 
(4)4(x-3)2-36=0 (5)(x-3)2=2(x-3)
|
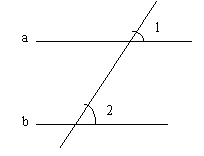
19、已知：如图，直线a,b被c所截，∠1，∠2是同位角，且∠1≠∠2,
求证：a不平行b
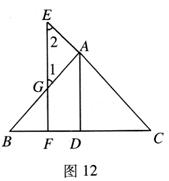
20、已知：如图12，AD⊥BC于D，EF⊥ BC于F，交AB于G，交CA延长线于E,∠ 1＝∠2．求证：AD平分∠ BAC，填写分析并写出证明过程．
分析：要证明AD平分∠ BAC，只要证明__________＝_______________，
而已知∠ 1＝∠ 2，所以应联想这两个角分别和∠ 1、∠ 2的关系，由已知BC的两条垂线可推出________∥_________，这时再观察这两对角的关系已不难得到结论．
21.用反证法证明:如果一个三角形的两个角不相等，那么这两个角所对的边也不相等。
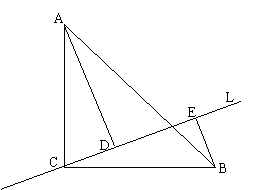
22．如图：已知等腰直角三角形ABC中,∠ACB=
,直线
经过点C,AD⊥,BE⊥,垂足分别为D、E。
(1)猜测AD，BE，DE三条线段的关系，并证明你的猜测。
(2)如图，当直线经过ΔABC内部时,其他条件不变,这个结论还是真命题吗?如果是真命题,请给出证明；如果是假命题，请说明理由。
 |
| 金色纸边
|
23.一张宽50cm，长80cm的矩形风景图片，要在它的四周镶上同样宽的金色纸边，
如果要使金色纸边的面积是矩形风景图片面积的75%，金色纸边的宽应是多少？
25如图,某地规划在一个长40m,宽26m的矩形场地ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种草,要使每一块草坪的面积都为144m2,那么通道的宽应设计成多少m?
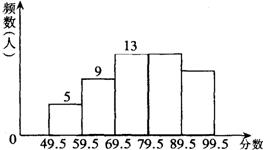
26．某中学八年级共有400名学生，学校为了增强学生的国防意识，在本年级进行了一次国防知识测验．为了了解这次测验的成绩状况，从中抽取了50名学生的成绩，将所得数据整理后，画出频数分布直方图如图所示．
(1)补充完整频数分布直方图
(2)图中第四个小组频数是多少?第四个小组频率是多少?
(3)这次测验中，八年级全体学生成绩在59.5～69.5中的人数约是多少?
（4）这50名学生分数的极差是多少？
(5)试估计这次测验中，八年级全体学生的平均成绩?
| 组别 | 分组 | 频数 | 频率 |
| 1 | 89.5~99.5 | 4 | 0.04 |
| 2 | 99.5~109.5 | 3 | 0.03 |
| 3 | 109.5~119.5 | 46 | 0.46 |
| 4 | 119.5~129.5 | b | c |
| 5 | 129.5~139.5 | 6 | 0.06 |
| 6 | 139.5~149.5 | 2 | 0.02 |
|
| 总计 | a | 1.00 |
27当竖直向上发射一枚火箭时,火箭的高度h(米)可以用公式h=-5t2+150t+10表示,其中t(秒)表示火箭发射后经过的时间,问火箭发射后何时能达到1010米高?
28. 为了了解初三毕业班学生的一分钟跳绳次数的情况,某校 抽取了一部分初三毕业生进行一分钟跳绳次数的测试,将所得数据进行处理,可得频数分布表.(1)在这个问题中,总体是___________________________________样本容量a=_______
(2)第四小组的频数b=______,频率c=______
(3)若次数在110次(含110次)以上为达标,试估计该校初三毕业生一分钟跳绳次数的达标率是多少?
(4)在这次测试中,学生跳绳次数
的中位数和众位数分别是什么?落在哪个小组内?
（5）根据上述频数分布表画出相应的频数分布折线图。
(6)说出在频数分部折线图中的虚设组是什么?
29. 为了调查初二学生的身高,抽取了一个个容量为25的样本(单位:厘米)如下:142，154，159，175，159，156，162，166，158，159，156，166，160，164，155，157，146，147，161，158，158，153，158，154，162，将上述数据
（1）列出频数分布表；（2）画出频数分布直方图
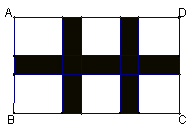
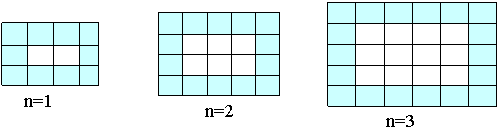
24、如图，用同样规格黑白两色的正方形瓷砖铺设长方形地面，请观察下列图形，并解答有关问题：
（1）设铺设地面所用瓷砖的总块数为y，请写出y与n（表示第n个图形）的关系式；
（2）上述铺设方案，铺一块这样的长方形地面共用了506块瓷砖，求此时n的值；
（3）黑瓷砖每块4元，白瓷砖每块3元，在问题（2）中，共需要花多少钱购买瓷砖？
（4）否存在黑瓷砖与白瓷砖块数相等的情形？请通过计算加以说明。
 |