紫帽中学2004－2005学年八年级下学期期中测试卷
(时间120分钟，满分150分)
| 题号 | 一 | 二 | 三 | 总分 | ||||||||
| 得分 | ||||||||||||
一、填空题：（每空2分，共54分）
1、81的平方根是 ，27的立方根是 。
2、函数
中自变量x的取值范围是 。
3、若
，则x=
。
4、如果
，那么
= 。
5、若
，则的取值范围是 。
6、平方根等于本身的数是 ，立方根等于本身的数是 。
7、用计算器计算
（精确到0.01）≈
。
8、比较大小：（1）
（2）
（填>,=,<）
9、若二次根式
与
是同类二次根式，则a= ，b=
。
10、点（2，－3）在第 象限。
11、若关于x的函数
是一次函数，则m= ，n
。
12、正比例函数
，当m
时，y随x的增大而增大。
13、双曲线
，经过点(3，k)，则k= 。
14、若函数
图象经过点（1，2），则m=
。
15、写出一条经过第一、二、四象限的直线的解析式y= 。
16、当k>0,b>0时，直线y=kx+b与双曲线y=的交点在第 象限。
17、已知函数
，当 
时，函数图象在第四象限。
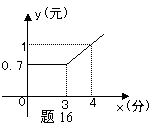18、在某公用电话亭打电话时，需付电话费y（元）与通话时间x（分钟）之间的函数关系用图象表示为图1，小明打了2分钟需付费 元；小莉打了8分钟需付费 元。
19、王华和张强同学在合作电学实验时，记录下电流I（安） 与电阻R（欧）有如下对应关系。
| R | …… | 2 | 4 | 8 | 10 | 16 | …… |
| I | …… | 16 | 8 | 4 | 3.2 | 2 | …… |
（1）观察上表，你认为I与R之间的函数关系式为： 。
（2）当电阻R＝5欧时，电流I＝ 安培。
二、选择题：（每小题都只有一个选项正确，每小题4分，共36分）
20、4的平方根是（ ）
A．
B．2 C．
D．
21、在实数
、
、0、
、
、
、
、
、2.……（不循环）中，无理数的个数为（
）
A、2个 B、3个 C、4个 D、5个
22、下列各式正确的是（ ）
A、=±6 B、 - =-2
C、=-6 D、=-
23、下列给出的四个点中，不在直线y=2x-3上的是（ ）
A、（1， -1） B、（0， -3） C、（2， 1） D、（-1，5）
24、在比例尺为1∶20000的地图上，量得甲、乙两地的距离为25cm，则两地的实际距离为（ ）
A、250000cm B、25km C、500km D、5km
25、点P（3，
）关于x轴对称的点的坐标是（ ）
A、（3，） B、（，）
C、（3，4）
D、（，4）
26、若
是正比例函数，则b的值是（ ）
A、0 B、
C、
D、
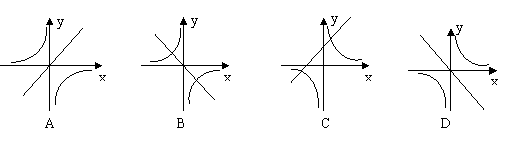
27、正比例函数
与反比例函数
在同一坐标系内的图象大致为（ ）
28、甲、乙两人同时从A地去学校，甲骑自行车，乙步行，用S表示甲、乙离学校的路程，t表示出发后的时间，能大致反映该事件的图象（ ）
 |
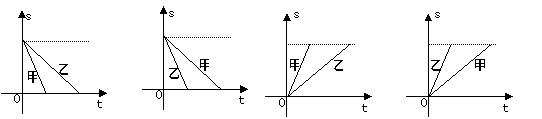A B C D
三、解答题：(共60分)
29、（本题6分）计算：－－＋
30、（本题6分）计算：
31、（本题8分）已知直线
经过点（1，2）和点（
，4），求这条直线的解析式。
32、（本题8分）一天上午8时，小华去县城购物，到下午2时返回家，结合图 像回答：
（1） 
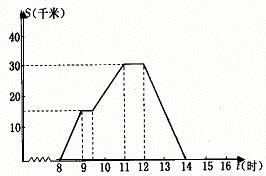小华何时第一次休息？
（2） 小华离家最远的距离是多少千米？
（3） 返回时平均速度是多少？
（4） 请你描述一下小华购物的情况。
33、（本题10分）已知直线
与直线
交于点A，且两直线分别与x轴交于B、C两点。
（1） 分别求出A、B、C三点的坐标，并画出两函数的图象。
（2） 
求△ABC的面积。
34、（本题10分）某公司到果园购买某种优质水果，果园对购买3000千克以上（含3000千克）的有两种销售方式，甲方案：每千克9元，由基地送货上门；乙方案：每千克8元，由顾客自己运回，已知该公司租车从基地到公司的运输费用是5000元
(1)分别写出该公司两种购买方案的付款y与所购买的水果量x之间的函数关系式；
(2)当购买量在什么范围时，选择哪种购买方式付款最少？
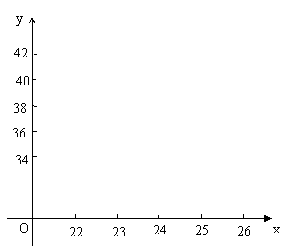
35、（本题12分）爱动脑筋的小明同学在买一双新的运动鞋时，发现了一些有趣现象，即鞋子的号码与鞋子的长（cm）之间存在着某种联系，经过收集数据，得到下表：
| 鞋长x（cm） | …… | 22 | 23 | 24 | 25 | 26 | …… |
| 码数y | …… | 34 | 36 | 38 | 40 | 42 | …… |
请你代替小明解决下列问题：
（1）根据表中数据，在同一直角坐标系中描出相应的点，你发现这些点在哪一种图形上？
（2）猜想y与x之间满足怎样的函数关系式，并求出y与x之间的函数关系式，验证这些点的坐标是否满足函数关系式。
（3）当鞋码是41码时，鞋长是多长？
 |