八年级数学第一章《勾股定理》练习题(无答案)

八年级数学第一章《勾股定理》练习题

一．　　　　　  选择题（10×4′=40′）

1．已知一个Rt△的两边长分别为3和4，则第三边长的平方是　　　　  （　　）

　　 A、25　　　　　　　　　　 B、14　　　　　　　　　C、7　　　　　　　　　 D、7或25

2．下列各组数中，以a，b，c为边的三角形不是Rt△的是　　　　　 （　　）

　　 A、a=1.5，b=2,c=3　　　 B、a=7,b=24,c=25

C、a=6,b=8,c=10　　　　　　D、a=3,b=4,c=5

3．若线段a，b，c组成Rt△，则它们的比为　　　　　　　　　　　　　 （　　）

　　 A、2∶3∶4　 B、3∶4∶6　 C、5∶12∶13　 D、4∶6∶7

4 . 直角三角形两直角边长分别为6cm和8cm,则连接这两条直角边中点的线段长为　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

(A)　　10cm　 (B)　　3cm　 (C)　 4cm　 (D)　 5cm

5. 在直角三角形中，斜边与较小直角边的和、差分别为8、2，则较长直角边长为　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

（A）　 5　　(B)　　 4 　　(C)　　3　　(D)　　 2

6．如果Rt△的两直角边长分别为n²－1，2n（n>1），那么它的斜边长是（　　）

　　 A、2n 　　B、n+1 　　C、n²－1　　D、n²+1

7．已知Rt△ABC中，∠C=90°，若a+b=14cm，c=10cm，则Rt△ABC的面积是（　　）

　　 A、24cm²　　B、36cm²　 C、48cm²　　D、60cm²

8．三角形的三边长为（a+b）²=c²+2ab,则这个三角形是　　　　　　　 ( 　　)

　 A. 等边三角形;　 B. 钝角三角形;　C. 直角三角形;　　D. 锐角三角形.

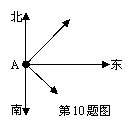
9．已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（　　）

　　 A、6cm²　　 B、8cm²　　 C、10cm²　　 D、12cm²

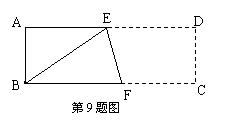10．已知，如图，一轮船以16海里/时的速度从港口A出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A出发向东南方向航行，离开港口2小时后，则两船相距（　　）

　　 A、25海里　　 B、30海里　　  C、35海里　　　D、40海里

二．填空题（9×4′=36′）

11．在Rt△ABC中，∠C=90°，①若a=5，b=12，则c=___________；②若a=15，c=25，则b=___________；③若c=61，b=60，则a=__________；④若a∶b=3∶4，c=10则S_Rt△ABC=________。

12．在由小方格组成的网格中，用数格子的方法判断出给定的钝角三角形和锐角三角形的三边不满足两边平方和等于第三边的平方，由此可想到________________________________________________。

13．直角三角形两直角边长分别为5和12，则它斜边上的高为__________。

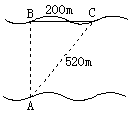
14.如图，某人欲横渡一条河，由于水流的影响，实际上岸地点C偏离欲

到达点B200m，结果他在水中实际游了520m，求该河流的宽度为_________。

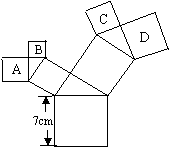
15．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边和长为7cm,则正方形A，B，C，D的面积之和为___________cm²。

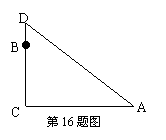16．在一棵树的10米高处有两只猴子，一只猴子爬下树走到离树20米处的池塘的A处。另一只爬到树顶D后直接跃到A处，距离以直线计算，如果两只猴子所经过的距离相等，则这棵树高_________________________米。

三．解答题（共24分）

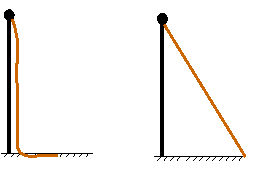17．（8分）小明想知道学校旗杆的高，他发现旗杆顶端的绳子垂到地面还多1米，当他把绳子的下端拉开5米后，发现下端刚好接触地面，求旗杆的高度。

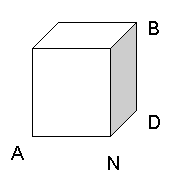18　　　  (8分)一块砖的宽AN=5，长ND=10,CD上的点B距地面

的高BD=8，地面上A处的一只蚂蚁要到B处吃食，需要

爬行的最短距离是多少？

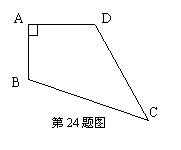24．（8分）已知，如图，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，且∠A=90°，求四边形ABCD的面积。