八年级数学练习卷
班级_________姓名____________
1、仔细观察下列图案，并按规律在横线上画出合适的图形．
2、下面的图形是由边长为l的正方形按照某种规律排列而组成的．
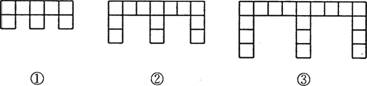
(1)观察图形，填写下表：
| 图形 | ① | ② | ③ |
| 正方形的个数 | 8 | ||
| 图形的周长 | 18 |
(2)推测第n个图形中，正方形的个数为________，周长为_______(都用含n的代数式表示)．
(3)这些图形中，任意一个图形的周长)，与它所含正方形个数石之间的函数关系式为______.
3、给出一个正方形，请你动手画一画，将它剖分为
个小正方形。那么，通过实验与思考，你认为这样的自然数可以取的所有值应该是_________________
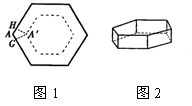4、将一块正六边形硬纸片（图1），做成一个底面仍为正六边形且高相等的无盖纸盒（侧面均垂直于底面，见图2），需在每一个顶点处剪去一个四边形，例如图1中的四边形AGA/H，那么∠GA/H的大小是
度。
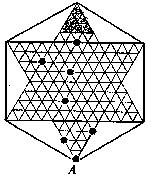
5、右图是跳棋盘，其中格点上的黑色点为棋子，剩余的格点上没有棋子，我们约定跳棋游戏的规则是：把跳棋棋子在棋盘内沿直线隔着棋子对称跳行，跳行一次称为一步。已知点A为己方一枚棋子，欲将棋子A跳进对方区域（阴影部分的格点），则跳行的最少步数为（ ）
（A）2步 （B）3步 （C）4步 （D）5步
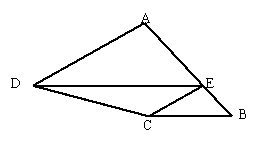6、如图，在四边形
中，
是
上一点，
∥
， 
∥
，若
，
，则
等于（ ）
A．
B．
C．
D．2
7、 两个完全相同的长方体的长、宽、高分别为5cm，4cm，3cm.把它们叠放在一起组成一个新长方体，在这些新长方体中，表面积最大是（ ）
A 188cm2 B 176cm2 C 164 cm2 D 158 cm2
8、依据闯关游戏规则，请你探究“闯关游戏”的奥秘：
（1）用列表的方法表示有可能的闯关情况；
（2）求出闯关成功的概率.
9、我市某乡规定：种粮的农户均按每亩年产量750公斤、每公斤售价1．1元来计算每亩的年产值．年产值乘农业税的税率就是应缴的农业税，另外还要按农业税的20%上缴“农业税附加”(“农业税附加”主要用于村级组织的正常运转需要)．
(1)去年我市农业税的税率为7％，王老汉一家种了10亩水稻，他一共要上缴多少元?
(2)今年，国家为了减轻农民负担，鼓励种粮，降低了农业税税率，并且每亩水稻由国家直接补贴20元(可抵缴税款)．王老汉今年仍种10亩水稻，他掰着手指一算，高兴地说：“这样一减一补，今年可以比去年少缴497元．”请你求出今年我市的农业税的税率是多少?(要有解题过程)
10、某生活小区的居民筹集资金1600元，计划在一块上、下底分别为10m，20m的梯形空地上种植花木（如图10-1）
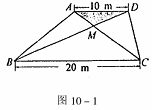（1）他们在△AMD和BMC地带上种植太阳花，单价为8元/m2，当△AMD地带种满花后（图10-1中阴影部分），共花了160元，请计算种满△BMC地带所需的费用.
11、探索下列问题：
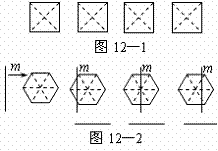
（1）在图12—1给出的四个正方形中，各画出一条直线（依次是：水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线），将每个正方形都分割成面积相等的两部分；
（2）一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2.
①请你在图12—2中相应图形下方的横线上分别填写S1与S2的数量关系式（用“<”，“=”，“>”连接）；
②请你在图12—3中分别画出反映S1与S2三种大小关系的直线n，并在相应图形下方的横线上分别填写S1与S2的数量关系式（用“<”，“=”，“>”连接）.
（3）是否存在一条直线，将一个任意的平面图形（如图12—4）分割成面积相等的两部分，请简略说出理由.
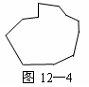
12、如图15—1和15—2，在20×20的等距网格（每格的宽和高均是1个单位长）中，Rt△ABC从点A与点M重合的位置开始，以每秒1个单位长的速度先向下平移，当BC边与网的底部重合时，继续同样的速度向右平移，当点C与点P重合时，Rt△ABC停止移动.设运动时间为x秒，△QAC的面积为y.
（1）如图15—1，当Rt△ABC向下平移到Rt△A1B1C1的位置时，请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形；
（2）如图15—2，在Rt△ABC向下平移的过程中，请你求出y与x的函数关系式，并说明当x分别取何值时，y取得最大值和最小值？最大值和最小值分别是多少？
（3）在Rt△ABC向右平移的过程中，请你说明当x取何值时，y取得最大值和最小值？最大值和最值分别是多少？为什么？
13、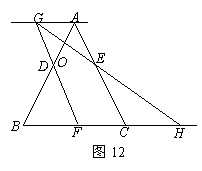
已知：如图12，等边三角形ABC的边长为6，点D，E分别在边AB，AC上，且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动，设点F运动的时间为t秒.当t>0时，直线FD与过点A且平行于BC的直线相交于点G，GE的延长线与BC的延长线相交于点H，AB与GH相交于点O.
（1）设△EGA的面积为S，写出S与t的函数关系式；
（2）当t为何值时，AB⊥GH；
（3）请你证明△GFH的面积为定值；
（4）当t为何值时，点F和点C是线段BH的三等分点.