人教实验版八年级(上)数学单元目标检测题（十四）
期末复习（二）
班级 姓名 号次
一、精心选一选（本题共10题，每题3分，共30分）
1、函数y=
中，字母的取值范围是（ ）
Ａ、a<1 Ｂ、a≤1 Ｃ、a≥1 Ｄ、a>1
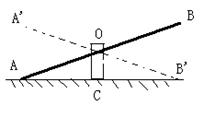
2、如图是跷跷板的示意图，支柱ＯＣ与地面垂直，点Ｏ是横板ＡＢ的中点，ＡＢ可以绕着点Ｏ上下转动，当Ａ端落地时，∠ＯＡＣ＝２０°，横板上下可转动的最大角度（即∠Ａ’OA）是（ ）
Ａ、８０° Ｂ、６０° Ｃ、４０° Ｄ、２０°
3、下列运算错误的是（ ）
A．
B．
C．
D．
4、将直线
向上平移两个单位，所得的直线是（ ）
A．
B．
C．
D．
5、上图可以看作是一个等腰直角三角形旋转若干次而生成的，则每次旋转的度数可以是（ ）
A．
B．
C．
D．
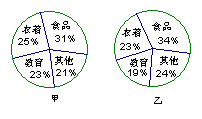
6、.右图是甲、乙两户居民家庭全年支出费用的扇形统计图。
根据统计图，下面对全年食品支出费用判断正确的是（ ）
A、甲户比乙户多 B、乙户比甲户多
C、甲、乙两户一样多 D、无法确定哪一户多
7、用一水管向图中容器内持续注水，若单位时间内注入的水量保持不变，则在注满容器的过程中，容器内水面升高的速度( )
A、保持不变 B、越来越慢
C、越来越快 D、快慢交替变化
8、一张正方形纸片经过两次对折，并在如图位置上剪去一个小正方形，打开后是( )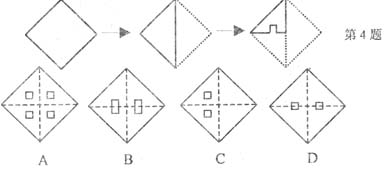 
9、在直角坐标系中，A（1，2）点的横坐标乘以－1，纵坐标不变，得到A’点，则A与A’的关系是（ ）
A、关于x轴对称 B、关于y轴对称 C、关于原点对称 D、将A点向x轴负
10、若M
、N
、P
三点都在函数
（ｋ＜0）的图象上，则
的大小关系为（ ）
A、
＞
＞
B、＞＞ C、＞＞ D、＞＞
二、耐心填一填（本题共8题，每题4分，共32分）
11、分解因式：4
－1＝______________________
12、如图，等腰
的顶角为
，腰长为10，则底边上的高AD=__________。
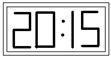
13、在平面镜里看到背后墙上,电子钟示数如图所示,这时的实际时间应该是______.
14、写出一个图象经过点(-1,-1),且不经过第一象限的函数表达式
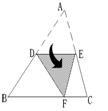
15、如图，D、E为△ABC两边AB、AC的中点，将△ABC沿线段DE折叠，使点A落在点F处，若∠B=55°，则∠BDF= °.
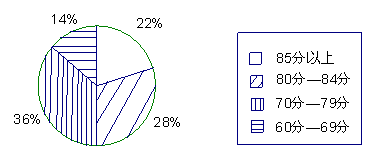
16、如图是某校九年级一班50名学生的一次数学测验成绩的扇形统计图，按图中划分的分数段，这次测验成绩中所占百分比最大的分数段是_________________；85分以上的共有____________人．
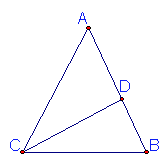
17、如图，等腰三角形ABC中，AB=AC，∠A=44°，CD⊥AB于D，则∠DCB等于 度
18、参加保险公司的医疗保险，住院治疗的病人享受分段报销，保险公司制定的报销细则如下表.某人住院治疗后得到保险公司报销金额是1000元，那么此人住院的医疗费是 元
| 住院医疗费（元） | 报销率（%） |
| 不超过500元的部分 | 0 |
| 超过500～1000元的部分 | 30 |
| 超过1000～3000元的部分 | 45 |
| …… |
三、细心做一做（本题共38分）
19、先化简，再求值。
20、下面的方格纸中，画出了一个“小猪”的图案，已知每个小正方形的边长为1．
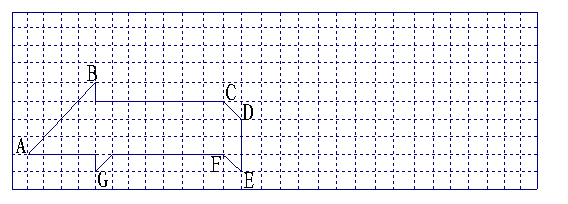（1）“小猪”所占的面积为多少？
（2）在上面的方格纸中作出“小猪”关于直线DE对称的图案（只画图，不写作法）；
（3）以G为原点，GE所在直线为x轴，GB所在直线为y轴，小正方形的边长为单位长度建立直角坐标系，可得点A的坐标是（_______，_______）．
21、某产品每件成本10元，试销阶段每件产品的日销售价
（元）与产品的日销售量
（件）之间的关系如下表：
|
| 15 | 20 | 25 | 30 | … |
|
| 25 | 20 | 15 | 10 | … |
（1）
请在直角坐标系上描点，观察点的颁布，建立与的恰当函数模型。
（2） 若要求每天卖出24件，则这一天它能获利多少元？
22、右图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图。
（1）求该班有多少名学生？
（2）补上步行分布直方图的空缺部分；
（3）在扇形统计图中，求骑车人数所占的圆心角度数。
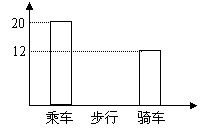（4）若全年级有500人，估计该年级步行人数。
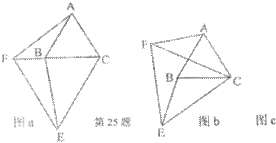23、如图a，⊿ ABC和⊿CEF是两个大小不等的等边三角形，且有一个公共顶点C，连接AF和BE.
(1)线段AF和BE有怎样的大小关系?请证明你的结论；
(2)将图a中的△CEF绕点C旋转一定的角度，得到图b，(1)中的结论还成立吗?作出判断并说明理由；
(3)若将图a中的△ABC绕点C旋转一定的角度，请你画山一个变换后的图形c(草图即可)，(1)中的结论还成立吗?作出判断不必说明理由；
(4)根据以上证明、说理、画图，归纳你的发现.
评价十四
一、CCBAC DCABA 二、11、（2x－1）（2x+1） 12、5 13、21：05 14、y=2x－3
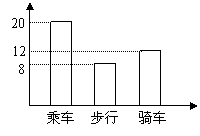15、70°
16、70～ 79 11 17、22 18、2889 三、19 、
20、（1）32.5 (2)略 (3)－4,0 21、（1）y=40－x
（2） 144 22、（1）40人
（2）见直方图
（3）圆心角度数=
=108º
（4）估计该年级步行人数=500×20%=100
23、（1）AF=BE 证明⊿ACF≌⊿BCE
（2）成立，证明⊿ACF≌⊿BCE
（3）同样成立。
（4）图形绕着C点旋转任意角度，上述结论均成立。