八年级数学第二学期期末考试试卷（1）
一、填空题（每小题2分，共30分）
1.
不等式
的解集是_________.
2.
分解因式：
___________.
3.
计算：
_____.
4. 写出一个分子至少含有两项，且能够约分的分式__________.
5.
当x =_____时，分式
的值为0.
6.
不等式组
的解集为___________.
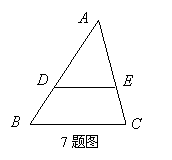
7. 如图，在△ABC中，DE∥BC，AD = 4，DB = 2，DE = 3，则BC =______.
8.
在比例尺为1:10
000的安阳工学院的学院平面图上，校园面积约为7060 cm
，则安阳工学院的实际占地面积约为_______ 万平方米.
9. 宽与长的比等于黄金比的矩形也称为黄金矩形，若一黄金矩形的长为2 cm，则其宽为_________ cm.
10. 已知
，则
=______.
11. 晚上，小明站在离路灯底部7米远的地方，测得他的影长为3米，若小明身高1.8米，则路灯的高为______米.
12. 已知：
，
，则
的值为_____.
13. 如图△ABC中，AB = AC，BD平分∠ABC，且△ABC ∽△BDC，则∠A =___度.
14. 如图，将①∠BAD = ∠C；②∠ADB = ∠CAB；③
；④
；⑤
；⑥
中的一个作为条件，另一个作为结论，组成一个真命题，则条件是__________，结论是_________.（注：填序号即可）
15. 
如图表示一艘轮船和一艘快艇沿相同路线从A港出发到B港行驶过程中路程随时间变化的图象，从图中可以看出，快艇出发_____小时后追上轮船.
二、选择题（每小题3分，共18分）
16. 下列两个图形：①两个等腰三角形；②两个直角三角形；③两个正方形；④两个矩形；⑤两个菱形 ；⑥两个正五边形. 其中一定相似的有（ ）.
A. 2组 B. 3组 C. 4组 D. 5组
17. 下列计算正确的是（ ）.
A. 
B.
C. 
D.
18. 在学校对学生进行的晨检体温测试中，学生甲连续10天的体温与36℃的上下波动数据为0.2、0.3、0.1、0.1、0、0.2、0.1、0.1、0、0.1，则在这10天中该学生的体温波动数据中不正确的是（ ）.
A. 平均数是0.12 B. 方差是0.02 C. 中位数是0.1 D. 众数是0.1
19. 方程
的解是（ ）.
A. 
B.
C.
D. 无解
20. 下列说法中：①两个图形位似也一定相似；②相似三角形对应中线的比等于对应周长的比；③一组数据的极差、方差或标准差越小，该组数据就越稳定； ④三角形的外角一定大于它的内角. 其中不正确的个数有（ ）.
A. 1个
B. 2个
C. 3个
D. 4个
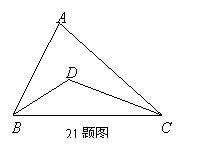
21. 如图所示，要判断△ABC 的面积是△DBC的
面积的几倍，只有一把仅有刻度的直尺，需要
度量的次数最少是（ ）.
A. 3次以上 B. 3次 C. 2次 D. 1次
三、解答题（22题7分，23题6分，24题7分，25题7分，共27分）
22. 解不等式组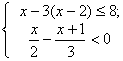
，并把解集表示在数轴上.
23. 因式分解：
24. 化简求值：
，其中
25. 解分式方程：
四、应用题（本题9分）
26. 为了保护环境，某企业决定购买10台污水处理设备. 现有A、B两种型号的设备，其中每台的价格、月处理污水量及年消耗费如下表：
| A型 | B型 | |
| 价格（万元/台） | 12 | 10 |
| 处理污水量（吨/月） | 240 | 200 |
| 年消耗费（万元/台） | 1 | 1 |
经预算，该企业购买设备的资金不高于105万元.
（1）请你设计该企业有几种购买方案；
（2）若企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案？
（3）在第（2）问的条件下，若每台设备的使用年限为10年，污水厂处理污水费为每吨10元，请你计算，该企业自己处理污水与将污水排到污水厂处理相比较，10年节约资金多少万元？（注：企业处理污水的费用包括购买设备的资金和消耗费）
五、（27题8分, 28题8分，共16分）
27. 在育才中学举行的电脑知识竞赛中，将初三两个班参赛学生的成绩（得分均为整数）进行整理后分成五组，绘制出如下的频数分布直方图（如图）.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30、0.15、0.10、0.05，第二小组的频数是40.
（1） 求第二小组的频率，并补全这个频数分布直方图；
（2） 求这两个班参赛的学生人数是多少；
（3） 
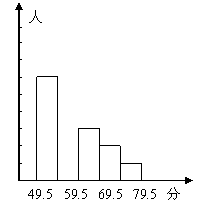这两个班参赛学生的成绩的中位数应落在第几小组内（不必说明理由）？
28. 已知：如图，点D、E分别在△ABC的边AB、AC上，且AD = 2DB，AE = 2EC.
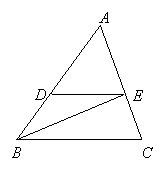求证：∠DEB = ∠EBC.
附加题（1题4分，2题6分，共10分）
1. 初次见面通常以握手示礼，适当的握手时间与力度会让人有一种舒服亲切的感受. 某次联谊会有41人参加，若41位与会人员彼此握手一次，那么全体与会人员共握手多少次？其实要解决这个问题，可以作以下的分析：假若用点来表示每个人，连接两点的线段数目表示握手的次数，
|
| 握手人数 | 握手次数 | ||
|
| 2 | 1 | ||
|
| 3 | 3 | ||
|
| 4 | 6 | ||
|
| 5 | 10 | ||
| … | … | … |
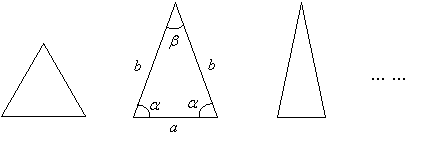
2. 如图，这些等腰三角形与正三角形的形状有差异，我们把它与正三角形的接近程度称为“正度”. 在研究“正度”时，应保证相似三角形的“正度”相等.
设等腰三角形的底和腰分别为a、b，底角和顶角分别为
、
，要求“正度”的值是非负数.
同学甲认为：可用式子
来表示“正度”，的值越小，表示等腰三角形越接近正三角形；
同学乙认为：可用式子
来表示“正度”，的值越小，表示等腰三角形越接近正三角形.
探索：（1）他们的方案那个较为合理，为什么？
（2）请你再给出一种衡量“正度”的表达式.