2005学年八年级(上)数学期末考试卷
(考试时间:100分钟)
一. ![]() 基本知识与基本技能(本题有10小题,每小题3分,共30分)。
基本知识与基本技能(本题有10小题,每小题3分,共30分)。
1.在函数y= 中,自变量的取值范围是________。
2.点P(-5,1)沿x轴正方向平移2个单位,再沿y轴负方向平移4个单位,所得到的点的坐标为_______。
3.三角形三边长分别为4,1-2a,7,则a的取值范围是
4.写一个图象经过点(-1,2),并y随x的增大而增大的一次函数的解析式_______________。
5.有10个数据的平均数为6,另有20个数据的平均数为3,那么所有这30个数据的平均数是________。
6.若直线y=kx+b经过第一、二、四象限,则k,b的取值范围是k____0,b____0。
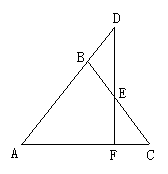
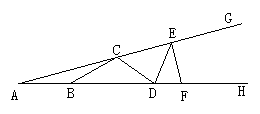 7.如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数是________。
7.如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数是________。
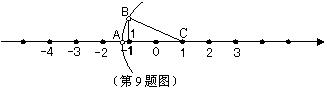 |
|
8.已知关于x的不等式组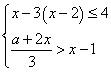 的解集是
的解集是![]() ,则a=_________。
,则a=_________。
9.如图,已知CA=CB,说出数轴上点A所表示的数是____。
 10.如图所示,用一根长度足够的长方形纸带,
10.如图所示,用一根长度足够的长方形纸带,
先对折长方形得折痕l,再折纸使折线过点B,
且使得A在折痕l 上,这时折线CB与DB
所成的角为: 。
二、谁的命中率高(本题有10小题,每小题3分,共30分).
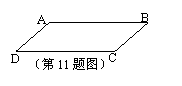 11.如图,若AB∥CD,则有①∠A+∠B=180O②∠B+∠C=180O③∠C+∠D=180O;上述结论正确的是 ( )
11.如图,若AB∥CD,则有①∠A+∠B=180O②∠B+∠C=180O③∠C+∠D=180O;上述结论正确的是 ( )
A.只有① B.只有②
C.只有③ D.只有①和③
12.分析下列说法,正确的有 ( )种。
①长方体、正方体都是棱柱; ②三棱柱的侧面是三角形;③圆锥的三视图中:主视图、左视图是三角形,俯视图是圆; ④球体的三种视图均为同样大小的图形;⑤直六棱柱有六个侧面、侧面为长方形。
A.2 B.3 C.4 D.5
13.下列命题错误的是 ( )
A.等腰三角形两腰上的中线相等 B.等腰三角形两腰上的高相等
C.等腰三角形的中线与高重合
D.等腰三角形顶角平分线上任一点到底边两端点的距离相等
14.下列各点中,不在函数y=2x+1的图象上的是 ( )
|
C.(-![]() ,0 )
D.(-1,3)
,0 )
D.(-1,3)
15.八年级(1)班50名学生的年龄统计结果如右表所示:
则此班学生年龄的众数、中位数分别为 ( )
A.14,14 B.15,14 C.14,15 D.15,16
 16.已知x轴上的点P到y轴的距离为3,则点P的坐标为( )
16.已知x轴上的点P到y轴的距离为3,则点P的坐标为( )
A.(3,0) B.(0,3) C.(0,3)或(0,-3) D.(3,0)或(-3,0)
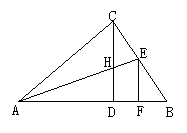
17.如图,Rt△ABC中,CD是斜边AB上的高,
 角平分线AE交CD于H,EF⊥AB于F,则下列
角平分线AE交CD于H,EF⊥AB于F,则下列
结论中不正确的是( )
A.∠ACD=∠B B.CH=CE=EF
C.CH=HD D.AC=AF
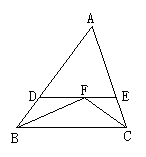
18.如图,△ABC中,∠ABC与∠ACB的平分线
交于点F,过点F作DE∥BC交AB于点D,交AC
于点E,那么下列结论:
①△BDF和△CEF都是等腰三角形; ②DE=BD+CE;
③△ADE的周长等于AB与AC的和; ④BF=CF.
其中正确的有 ( )
A.①②③ B.①②③④ C.①② D.①
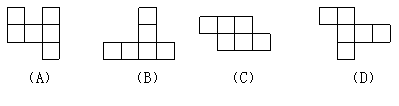 19.下列各图中能折成正方体的是
( )
19.下列各图中能折成正方体的是
( )
20.已知点A(a+2,5)、B(-4,1-2a),若AB平行于x轴,则a的值为( )
A.-6 B.2 C.3 D.-2
三.解答题(本题有7小题,共60分)
21.(10分)已知一次函数的图象经过点A(-3,4),B(-1,-2)。
(1)求出这个一次函数的解析式,并作出它的图象
(2)求△AOB的的面积.
(3)由图象观察,当-4≤x≤1时,函数y的变化范围
22.(6分)解不等式组,并在数轴上表示解集。
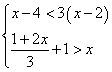
 |
23.(6分)画出右图几何体的三种视图。
 |
24.(8分)如图,△ABC中BA=BC,点D是AB
延长线上一点,DF⊥AC于F交BC于E,
求证:△DBE是等腰三角形.
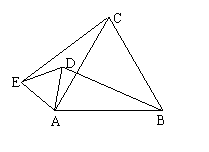 25.(8分)如图所示,若△ABC、△ADE都是
25.(8分)如图所示,若△ABC、△ADE都是
正三角形,请试比较:线段BD与线段CE的大
小?写出你的猜想,并说明理由.
26.(10分)某中学八年级(12)班同学利用勤工俭学收入的66元钱,同时购买单价分别为3元、2元、1元的甲、乙、丙三种纪念品,奖励参加校“元旦会演”活动的同学。已知购买乙种纪念品件数比购买甲种纪念品的件数多2件,而购买甲种纪念品的件数不少于10件,且购买甲种纪念品的费用不超过总费用的一半,若购买的甲、乙、丙三种纪念品恰好用了66元钱,问可有几种购买方案?每种方案中购买的甲、乙、丙三种纪念品各有多少件?
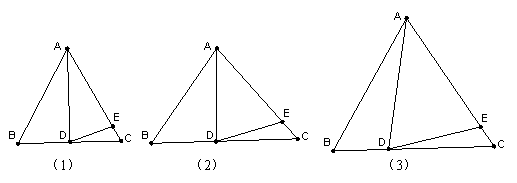
27.(12分)在ΔABC中,AB=AC
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=__________
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=__________
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:____________________
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,
请你写出来,并说明理由(6分)
 |
 2005年上学期麻车初中八年级数学期末考试答题卷
2005年上学期麻车初中八年级数学期末考试答题卷
| 题号 | 1-10 | 11-20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 总分 |
| 得分 |
一、基本知识与基本技能(本题有10小题,每小题3分,共30分)。
1、____ 2、 3、 4、 5、 6、 ,_____
7 8 9 10
二、谁的命中率高(本题有10小题,每小题3分,共30分).
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 选项 |
三.解答题(本题有7小题,共60分)
21、
22、
23、
 24、
24、
25、
| |
27、解:(1)∠EDC=______; (2)∠EDC=______; (3)______________。
(4)
参考答案以及评分标准
一、基本知识与基本技能(本题有10小题,每小题3分,共30分)。
1、![]() ;
2、(-3,-3); 3、
;
2、(-3,-3); 3、![]() ; 4、答案不唯一,符合题意即可; 5、 4 ; 6、 < , > ; 7、
; 4、答案不唯一,符合题意即可; 5、 4 ; 6、 < , > ; 7、![]() ;
8、 0 ;
;
8、 0 ;
9、![]() ;
10、
;
10、![]() 。
。
二、谁的命中率高(本题有10小题,每小题3分,共30分).
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 选项 | B | C | C | D | B | D | C | A | D | D |
三.解答题(本题有7小题,共60分)
21.(12分)已知一次函数的图象经过点A(-3,4),B(-1,-2)。
(1)求出这个一次函数的解析式,并作出它的图象
(2)求△AOB的的面积.
(3)由图象观察,当-4≤x≤1时,函数y的变化范围
解:(1)设这个一次函数的解析式为![]() ,则:
(1分)
,则:
(1分)
![]()
![]() (1分)
(1分)
![]() 解得
解得 ![]() (2分)
(2分)
∴这个一次函数的解析式是![]() (1分)
(1分)
作出正确的图象 (2分)
(2)作AM⊥y轴于M,作BN⊥轴于N,则△AOB的的面积为:
![]() (1分)
(1分)
![]() (1分)
(1分)
∴△AOB的的面积为 (1分)
(3)由图象可知,当-4≤x≤1时,函数y的变化范围是![]() (2分)
(2分)
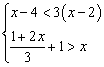 22.(5分)解不等式组,并在数轴上表示解集。
22.(5分)解不等式组,并在数轴上表示解集。
解:解第一个不等式得![]() (1分)
(1分)
解第二个不等式得![]() (1分)
(1分)
∴原不等式组的解为![]() (1分)
(1分)
正确把不等式的解表示在数轴上 (2分)

 23.(5分)画出右图几何体的三种视图。
23.(5分)画出右图几何体的三种视图。
24.(8分)如图,△ABC中BA=BC,点D是AB
延长线上一点,DF⊥AC于F交BC于E,
求证:△DBE是等腰三角形.
解:∵DF⊥BC,∴∠D+∠A=90O,∠FEC+∠C=90O, (2分)
∵BA=BC,∴∠A=∠C (1分)
∴∠D=∠FEC (2分)
又∵∠FEC=∠BED,∴∠D=∠BED (2分)
∴△DBE是等腰三角形. (1分)
 25.(8分)如图所示,若△ABC、△ADE都是
25.(8分)如图所示,若△ABC、△ADE都是
正三角形,请试比较:线段BD与线段CE的大
小?写出你的猜想,并说明理由.
解:BD=CE,理由如下: (1分)
∵△ABC、△ADE是正三角形,
∴AB=AC,AD=AE (2分)
∴∠EAD=∠CAB=60O (1分)
∴∠EAC=EAD+∠CAD=60O+∠CAD=∠CAB+∠CAD(1分)
∴△ABD≌△ACE (2分)
∴BD=CE (1分)
26.(10分)某中学八年(12)班同学利用勤工俭学收入的66元钱,同时购买单价分别为3元、2元、1元的甲、乙、丙三种纪念品,奖励参加校“元旦会演”活动的同学。已知购买乙种纪念品件数比购买甲种纪念品的件数多2件,而购买甲种纪念品的件数不少于10件,且购买甲种纪念品的费用不超过总费用的一半,若购买的甲、乙、丙三种纪念品恰好用了66元钱,问可有几种购买方案?每种方案中购买的甲、乙、丙三种纪念品各有多少件?
解:设购买甲、乙、丙三种纪念品分别为![]() 件,由题设可知 (1分)
件,由题设可知 (1分)
![]()
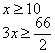
![]() ,∴
,∴![]() (4分)
(4分)
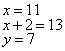
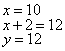 且
且![]()
![]() (2分)
(2分)
![]()
![]() ∴
或
(2分)
∴
或
(2分)
∴可有两种购买方案:购买甲、乙、丙纪念品分别为10、12、12件
或11、13、7件。 (1分)
27.(12分)在ΔABC中,AB=AC(每空1分)
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC= 15O
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC= 20O
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:∠BAD=2∠EDC(或![]() )
)
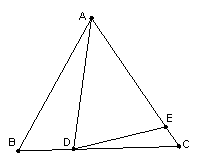 (4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,
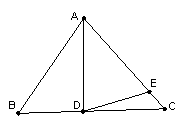
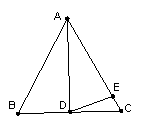 请你写出来,并说明理由(9分)
请你写出来,并说明理由(9分)
|
|
|
解:仍成立,理由如下 (1分)
∵AD=AE,∴∠ADE=∠AED, (1分)
∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=(∠EDC+∠C)+∠EDC
=2∠EDC+∠C (5分)
又∵BA=BC,∴∠B=∠C (1分)
∴∠BAD=2∠EDC。 (1分)