第四、五章测试卷
班级 学号 姓名 得分
一、选择题:(每题3分,共30分)
1、下列语句不是命题的是( )
A、两点之间线段最短 B、不平行的两条直线有一个交点
C、x与y的和等于0吗? D、对顶角不相等。
2、命题:①对顶角相等;②垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中假命题有( )
A、1个 B、2个 C、3个 D、4个
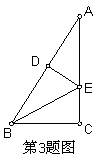 3、如图,△ABC中,
3、如图,△ABC中,![]() ,BE平分∠ABC,
,BE平分∠ABC,![]() ,垂足
,垂足
为D,如果![]() ,那么
,那么![]() 的值为( )
的值为( )
A、2㎝ B、3㎝ C、5㎝ D、4㎝
4、下列各组所述几何图形中,一定全等的是( )
A、一个角是45°的两个等腰三角形
B、两个等边三角形
C、腰长相等的两个等腰直角三角形
D、各有一个角是40°,腰长都为5㎝的两个等腰三角形
 5、等腰三角形的一个外角是80°,则其底角是( )
5、等腰三角形的一个外角是80°,则其底角是( )
A、40° B、100°或40° C、100° D、80
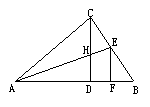
6、如图,Rt△ABC中,CD是斜边AB上的高,角平分线AE交CD于H,
EF⊥AB于F,则下列结论中不正确的是( )
A、∠ACD=∠B B、CH=CE=EF C、AC=AF D、CH=HD
7.平行四边形的周长为24cm,相邻两边长的比为3:1,那么这个平行四边形较短的边长为( ).
(A)6cm (B)3cm (C)9cm (D)12cm
8.一个多边形的内角和等于外角和的一半,那么这个多边形是( )
(A)三角形 (B)四边形 (C)五边形 (D)六边形
9.在![]() ABCD中,∠A:∠B:∠C=2:3:2,则∠D=( )
ABCD中,∠A:∠B:∠C=2:3:2,则∠D=( )
(A)36° (B)108° (C)72° (D)60°
10.平行四边形的两条对角线分别为6和10,则其中一条边x的取值范围为( ).
(A)4<x<6 (B)2<x<8 (C)0<x<10 (D)0<x<6
二、填空题:(每空3分,共30分)
11.在![]() ABCD中,若∠A+∠C=120°,则∠A=_______,∠B=_________.
ABCD中,若∠A+∠C=120°,则∠A=_______,∠B=_________.
12.在![]() ABCD中,AB=4cm,BC=6cm,则
ABCD中,AB=4cm,BC=6cm,则![]() ABCD的周长为______ .
ABCD的周长为______ .
13.已知O是![]() ABCD的对角线交点,AC=24cm,BD=38cm,AD=28cm,则△AOD的周长是________.
ABCD的对角线交点,AC=24cm,BD=38cm,AD=28cm,则△AOD的周长是________.
14.把命题“同角的补角相等”改写成“如果……那么……”的形式是如果 ______________________________________,那么________________________________.
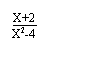 15.已知平行四边形的面积是144cm2,相邻两边上的高分别为8cm和9cm,则这个平行四边形的周长为________.
15.已知平行四边形的面积是144cm2,相邻两边上的高分别为8cm和9cm,则这个平行四边形的周长为________.
16.若x≠2,则分式 有意义为假命题.可举反例
 17.如图,在
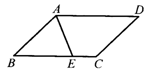
17.如图,在![]() ABCD中,∠A的平分线交BC于点E.若AB=10cm,AD=14cm,则BE=______,EC=________.
ABCD中,∠A的平分线交BC于点E.若AB=10cm,AD=14cm,则BE=______,EC=________.
(第17题) (第18题) (第19题)
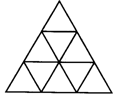
18.如图,用9个全等的等边三角形,按图拼成一个几何图案,从该图案中可找出____个平行四边形.
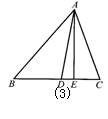
19.如图,AD,AE分别是△ABC的角平分线和高,∠B=50°,∠C=70°,则∠EAD=______.
|
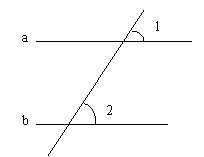 20、已知:如图,直线a,b被c所截,∠1,∠2是同位角,且∠1≠∠2,求证:a不平行b
20、已知:如图,直线a,b被c所截,∠1,∠2是同位角,且∠1≠∠2,求证:a不平行b
证明:假设 ,
则 ( )
这与 相矛盾,所以 不成立,所以a不平行b。
三、解答题(共40分)
21、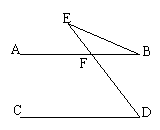 已知:E是AB、CD外一点,∠D=∠B+∠E,求证:AB∥CD.(6分)
已知:E是AB、CD外一点,∠D=∠B+∠E,求证:AB∥CD.(6分)
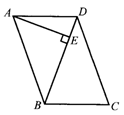
22.如图,在![]() ABCD中,DB=CD,∠C=70°,AE⊥BD于点E.试求∠DAE的度数.(6分)
ABCD中,DB=CD,∠C=70°,AE⊥BD于点E.试求∠DAE的度数.(6分)
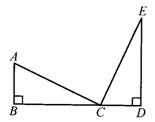
23.(6分)如图,已知AB⊥BD于点B,ED⊥BD于点D,且AB=CD,BC=DE,
求证(1)AC=CE (2)AC⊥CE
24. (6分)求证:等腰三角形的两底角平分线相等
25、如图在ΔABC中AB=AC,∠BAC=900,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F
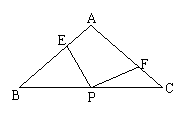 ⑴求证:AE=CF(提示:添辅助线)(4分)
⑴求证:AE=CF(提示:添辅助线)(4分)
⑵是否还有其他结论,不要求证明(至少2个,2分)
26、(本题有3小题,第(1)小题为必答题,满分6分;第(2)、(3)小题为选答题,其中,第(2)小题满分4分,第(3)小题满分6分,请从中任选1小题作答,如两题都答,以第(2)小题评分。)
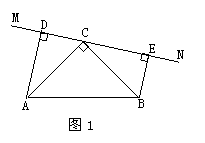
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
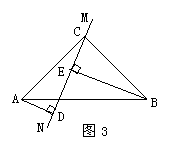
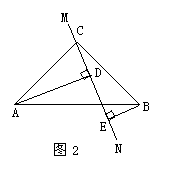 (3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
 | |||
 | |||
注意:第(2) 、(3)小题你选答的是第 小题.