初二（下）第一学月考试数学试卷(B)
内容：四边形全章 时间：90分钟
一、选择题：
1．下列说法：（1）四边形最多有3个钝角. (2) 四边形最多有3个锐角.
（3）四边形至少有1个钝角。（4）n边形的内角和能被180整除。
其中正确的有（ ） （A）1个 （B）2个 （C）3个 （D）4个
2．七边形的对角线的条数是（ ）
（A）10 （B）12 （C）14 （D）16
3．下列说法：（1）平行四边形的对角线互相平分。（2）菱形的对角线互相垂直平分。
（3）矩形的对角线相等，并且互相平分。（4）正方形的对角线相等，并且互相垂直平分。
其中正确的是（ ）
（A）①，②.（B）①，②，③.（C）②，③，④ （D）①，②，③，④
4.下列命题中,假命题是( )
(A)对角线互相平分且相等的四边形是矩形.(B)对角线相等的菱形是正方形.
(C)两邻边相等的平行四边形是正方形. (D)对角线互相垂直平分的四边形是菱形.
5.下列图形中,既是中心对称图形，又是轴对称图形的是( )
(A)平行四边形 (B)等边三角形 (C)矩形 (D)等腰梯形
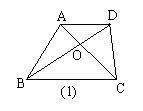
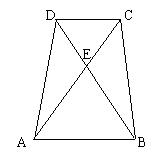
6．如图1，梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，
则图中面积相等三角形有（ ）
（A）1对 （B）2对 （C）3对 （D）4对
7．四边形ABCD的对角线相交于O点，能判定四边形是正方形的条件是（ ）
（A）AC=BD，AB=CD，AB∥CD。（2）AD∥BC，∠A=∠C。
（C）AO=BO=CO=DO，AC⊥BD。（D）AO=CO，BO=DO，AB=BC。
8．下列说法：①一组对边平行，另一组对边相等的四边形是平行四边形或等腰梯形。
②一组对边平行，一组对角相等的四边形是平行四边形。
③两组对角分别相等的四边形是平行四边形。
④顺次连结等腰梯形各边中点所得到的四边形是菱形。其中正确的是（ ）
（A）①②.（B）①②③.（C）②③④ （D）①②③④。
9．顺次连结四边形四条边的中点，所得的四边形是菱形，则原四边形一定是（ ）
（A）平行四边形.(B) 对角线相等的四边形.(C) 矩形.(D) 对角线互相垂直的四边形.
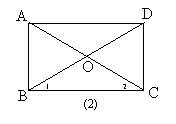10.如图2,矩形ABCD中,∠AOD=1200,
BC= 3
cm,则下列结论：
①∠2=300. ②AB=3 cm. ②AC==6cm. ④S矩形ABCD=9cm2.
(5) ΔAOB是等边三角形. 其中正确的有（ ）
（A）①②③.（B）①②③④.（C）②③④⑤.（D）①②③④⑤。
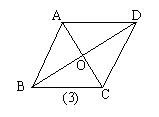11. 如图3,菱形ABCD的面积为2,∠ABC∶∠BAD=1∶2,则下列结论:
①∠ABC=600.②∠ABO=300.③ AC=2.④BD=2.⑤菱形ABCD的周长是8.
其中正确的有（ ）
（A）①②③④⑤.（B）①②③④.（C）②③④⑤.（D）①②③.
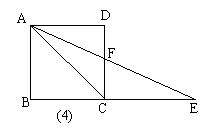12.如图4,正方形ABCD中,点E在BC的延长线上，AE平分∠DAC,则下列结论:
（1）∠E=22.50. (2) ∠AFC=112.50. (3) ∠ACE=1350.
（4）AC=CE。(5) AD∶CE=1∶
. 其中正确的有（ ）
（A）5个 （B）4个 （C）3个 （D）2个
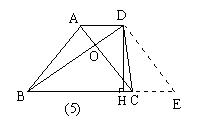13. 如图5，在梯形ABCD中，AD∥BC，AC⊥BD，AC=3cm，BD=4cm.
作DE∥AC，交BC的延长线于E，则下列结论:
(1) 四边形ACED是平行四边形. （2）∠BDE=∠BOC=900;
（3）BC+AD=BE=5cm;
(4)梯形ABCD的高DH=
=2.4cm,面积为 6cm2；
（５）S梯形ABCD=SΔBDE.。其中正确的有（ ）
（A）5个 （B）4个 （C）3个 （D）2个
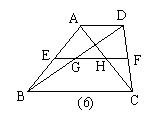
14.如图6，梯形ABCD中，AD∥BC，AH=HC,DG=GB，GH交两腰于E、F. 则下列结论:
(1)
AE=EB，DF=FC。 (2) AD∥EF∥BC.
(3)EH=GF=
BC,EG=HF=AD.(4)GH=
(BC-AD).
其中正确的有（ ）（A）1个 （B）2个 （C）3个 （D）４个
15．直角梯形的一个内角为
，较长的腰为6cm，一底为5cm，则这个梯形的面积为（ ）
（A）
.（B）
.（C）25
.（D）或.
二、填空：
16.若等腰梯形的周长为80cm, 高为12cm,中位线长与
腰长相等, 则它的面积为________cm2.
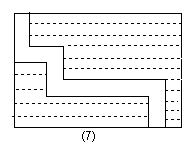
17.如图7，一块矩形场地,长为120米,宽为70米,
从中留出如图所示的宽为1米的小道,其余部分种草,
则草坪的面积为__________米2.
18．矩形ABCD的周长是14
，对角线相交于O，ΔAOD与ΔAOB的周长的差是1，那么这个矩形的面积是______。
19．平行四边形ABCD中，AB=6，BC=12，对边AD和BC的距离是4，则对边AB和CD间的距离是______。
20．菱形两对角线长分别为24和10，则菱形的高为______。
21．一个多边形除去一个内角外,其余内角的和为25700,则这个多边形的边数是____.
三、解下列各题：
22．如图，梯形ABCD中，DC∥AB，AC⊥BD，梯形的高为4，对角线AC=5，求梯形ABCD的面积。
23．如图，矩形ABCD的对角线相交于O，BE⊥DE，OF⊥DE。求证：点F是DE的中点。
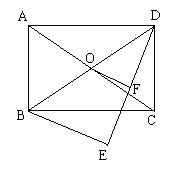
24．在平行四边形ABCD的对角线AC上截取AF=CE，作FH⊥BC，EG⊥AD。
求证：GH与EF互相平分。
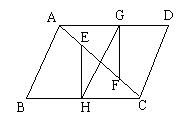
25．梯形ABCD中，AD∥BC，E、F分别是AD、BC的中点，∠B+∠C=900。求证：EF=（BC-AD）。
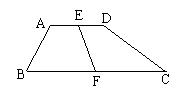
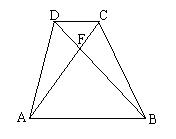
26． 如图，在正方形ABCD的对角线BD上取一点E，使BE=BC，过E点作FG⊥BD，FG与AD、DC相交于G、F。求证：DE=EF=FC。
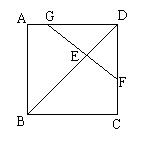
27.如图,梯形ABCD中, DC∥AB，对角线相交于E，∠AEB=600，AC=BD=24cm,AB=3DC，求梯形ABCD的周长和面积。
28．已知：如图，ΔABC中，AD是高，BE=EC，∠C=2∠B。求证：AC=2ED。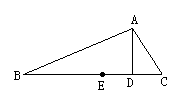
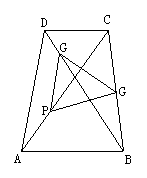
29. 如图, 等腰梯形ABCD中, DC∥AB，对角线相交于O，∠AOB=600，点P、Q、G分别是AO、BC、DO的中点。求证：ΔPQG是等边三角形。
参考答案:
一.
CCDC,CCCD,BDAA,ADD.
二.
16.240;
17.8211;
18.12cm2;
19.8cm;
20.
;
21.17.
三.
22.
作CG⊥AB于G,则CG=4,AG=3.
作CM∥DB,交AB的延长线于M,
则BM=DC,∠ACM=∠AFB=900.
设GM=x,CM=y,
由CM2+CA2=AM2及CM2－GM2=CG2得
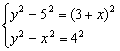
解得x=
.
∴S梯形ABCD=
×(DC+AB)×CG=×AM×CG=
.
23.
∵BE⊥DE,OF⊥DE,
∴BE∥OF,
∵矩形ABCD中,DO=OB,
∴DF=FE.
24.
连结EG、FH.
先证GF∥HE
再证ΔAGF≌ΔCHE,得GF=HE,
∴GEHF是平行四边形,
∴GH与EF互相平分.
25.
作EG∥AB,交BC于E;作EH∥DC,交BC于E.
∵AD∥BC,
∴四边形ABGE和EDCH是平行四边形.
∵AE=ED,
∴BG=AE=ED=CH,
∵BF=FC,
∴GF=FH,
∵∠B+∠C=900,∠B=EGH,∠C=∠EHG,
∴∠EGH+∠EHG=900,
∴∠GEH=900,
∴EF=×GH=(BC－2BG)= (BC－AD).
26.连EC.
∵ABCD是正方形,FG⊥BD,
∴∠BEC+∠CEF=∠BCE+∠ECF=900.
∵BE=BC,
∴∠BEC=∠BCE,
∴∠CEF=∠ECF,
∴EF=FC.
∵∠EDF=450，
∴∠EFD=450,
∴EF=ED,
∴EF=ED=FC.
27.
作CG∥DB,交AB的延长线于G.
∵梯形ABCD中,DC∥AB,
∴∠ACG=∠AEB=600,CG=DB=AC=24,
∴ΔACG是等边三角形,
∴AG=AC=24,
作CH⊥AG于H,则CH=12
,
∴S梯形ABCD=×AG×CH=144.
∵AB=3DC=3BG,AB+BG=24,
∴AB=18,BG=6,
∴BH=6,
∴BC=
∴梯形ABCD的周长=2BC+AG=(
+24)cm.
28.
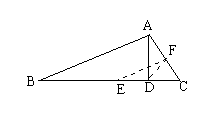
作AC的中点F,连FE,FD.
先证EF∥AB,DF=FC=AF,
∴∠EFC=∠B,∠C=∠FDC,
∵∠C=2∠B,
∴∠FDC=2∠FED,
∵∠FDC=∠FED+∠EFD,
∴∠FED=∠EFD,
∴DE=DF,
∴AC=2DF=2DE.
29.
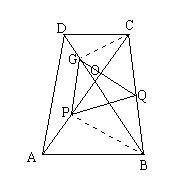
先证ΔDAB≌ΔCBA,
∴∠DBA=∠CAB,
∵∠AOB=600,
∴ΔAOB是等边三角形,
∵AP=PO,
∴BP⊥AO,
∵CQ=QB,
∴PQ=BC.
同理GQ=BC.
再证PG=AD.
∴PQ=QG=GP.
。