2005-2006学年八年级数学第二学期教学质量检测
| 题号 | 一 | 二 | 三 | 总 分 | |||||
| 1-10 | 11-20 | 21 | 22 | 23 | 24 | 25 | 26 | ||
| 得分 | |||||||||
注：1、可以使用计算器，但未注明精确度的计算问题不得采取近似计算，建议根据题型的特点把握好使用计算器的时机。
2、本试卷满分100分，在90分钟内完成。
一、选择题：（本题共10小题，每题3分，共30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
每题给出4个答案，其中只有一个是正确的，请把选出的答案编号填在上面的答题表中，否则不给分.
1、下列运算正确的是
A、
B、3
=3 C、
D、
2、下列各式化简，正确的是
A、
B、
C、
D、
3、下列二次根式中与
是同类二次根式的是
A、
B、
C、
D、
4、等式
成立的条件是
A、a≥0 B、a＞2 C、a≠2 D、
≥0
5、当1＜x＜3时，化简
的结果是
A、2x-4 B、-2 C、-4 D、2
6、在线段、正三角形、菱形、等腰梯形中，一定是中心对称图形的有
A、1个 B、2个 C、3个 D、4个
7、一个直角三角形的两条边是3cm和4cm，则第三边长是
A、5cm
B、
cm
C、5cm或cm D、不能确定
8、如果线段a、b满足
，那么
的值是
A、
B、
C、
D、
9、矩形具有，而菱形不一定具有的性质是
A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对边相等
10、如图，△ABC中，BD是∠ABC的平分线，DE∥AB交BC于E，已知EC＝3，BE＝2，则AB等于
A、
B、
C、6 D、4
二、填空题：（共10小题，每题3分，共30分，请将答案填入答题表中）
| 题号 | 11 | 12 | 13 | 14 | 15 |
| 答案 | |||||
| 题号 | 16 | 17 | 18 | 19 | 20 |
| 答案 |
11、一个正数的两个平方根分别为
和
，则a= .
12、计算：
＝ .
13、当x___时，
在实数范围内有意义.
14、2 -
的倒数是___（结果要求化简）.
15、在实数范围内分解因式
＝___.
16、把
根号外的因式移入根号内化简，得到的结果是___.
17、一个多边形的每一个内角等于144º，则它是___边形.
18、在Rt△ABC中，两条直角边长分别为6和8，则斜边上的中线为 .
19、在四边形ABCD中，AB=CD，要求再添加一个条件，使之可判定为平行四边形，请写出你添加的条件___（只要求写一种添法）
20、△ABC的三边分别为18、10、14，△DEF与△ABC相似，且它的最小边是5，则
△DEF的最长边是___.
三、解答题：（本部分共6题，其中第21-22题每题6分，第23-26题每题7分，共40分）
21、
解：原式=
22、
÷
·(-3
)（x>0，y>0）
解：原式=
23、化简并求值：
，其中
解：原式=
24、在四边形ABCD中，AB=DC，∠B=∠C<90º，求证：四边形ABCD是梯形.
证明：
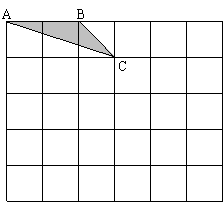
25、如图：在大小为6×5的正方形方格中，△ABC的顶点A、B、C在单位正方形的顶点上，请解答下列问题：
（1）在图中画一个△DEF ，使△DEF∽△ABC（相似比不为1），要求点D、E、F必须在单位正方形的顶点上（可以使用已用过的顶点）；
（2）写出它们对应边的比例式；并求△DEF与△ABC的相似比.
 |
26、如图：△ABC中，BD、CE是两条高，AM是∠BAC的平分线，且交DE于N，
求证：
证明：
2002-2003学年第二学期教学质量检测
初二数学参考评分标准
一、选择题：（本题共10小题，每题3分，共30分）
ACDBD BCACA
二、填空题：（共10小题，每题3分，共30分，请将答案填入答题表中）
11、5
12、3 13、小于0（<0，或x<0） 14、2 +
15、3(x+
)( x-)
16、-
17、10 18、5 19、AB//CD，或AD=BC 20、9
三、解答题：（本部分共6题，其中第21-22题每题6分，第23-26题每题7分，共40分）
21、解：原式= [-(-
)][+(-)]……………………………1分
= 3-(-)2……………………………………………………2分
= 3-(8-4) ……………………………………………………2分
= 4-5 …………………………………………………………1分
22、解：原式= -3
·
·……………………………1分
= -3
……………………………2分
=-3
……………………………2分
=
……………………………1分
23、解：原式=
………………………………………………2分
=
………………………………………………1分
= (x-1)2（此时代入和乘方后代入x的值都不扣分） …………………2分
当=
时
原式=(-1)2 = 5
………………………………………………2分
24、证法I：
作AE⊥BC于E、DF⊥BC于F ……………………………1分
证△ABE≌△DCF ……………………………2分
证AE=DF，又AE//DF
得四边形AEFD是平行四边形 ……………………………1分
∴AD//BC ……………………………1分
由∠B=∠C<90º，∴∠B+∠C<180º
∴AB不平行于DC ……………………………1分
（或∠B=∠C<90º，则E、F在线段BC上，得AD<BC，说明四边形ABCD不可能是平行四边形）
∴四边形ABCD是梯形 ……………………………1分
证法II：
作AE//CD交BC于E …………………………………………………1分
证AB=AE=DC …………………………………………………2分
证AB//DC
得四边形AECD是平行四边形 ………………………………………………1分
∴AD//BC ………………………………………………1分
由∠B=∠C<90º，∴∠B+∠C<180º
∴AB不平行于DC …………………………………………………1分
∴四边形ABCD是梯形 …………………………………………………1分
证法III：连结AC、BD证两次全等后得AD//BC……，请酌情给分。
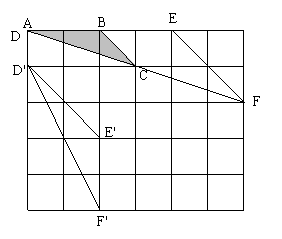
25、（1）类似于图中△DEF和△D'E'F'（其它情况酌情给分）……………3分
（2）注：图中字母标注的顺序可以不是A-D，B-E，C-F，但比例式中一定是对应边的比
；
………………………4分（其中相似比2分）
26、证明：证△AEC∽△ADB ……………………………………………………………1分
得AE·AB＝AD·AC ……………………………………………………………1分
证△ADE∽△ABC ……………………………………………………………1分
△ADN∽△ABM
…………………………………2分
又△ADE∽△ABC
…………………………………1分
得
……………………………………………………………1分
注：此题学生可能会用相似三角形角平分线的比与相似比的关系，请酌情给分。