反比例函数测试

反比例函数测试卷

（时间：100分钟　 满分：100分）

一、填空题（每题3分,共30分）

1.若双曲线y＝(m－1)x^－1在第一,三象限内,则m的取值范围是_______________

2.如果函数y＝kx^2k2＋k－2的图象是双曲线,且在第二,四象限内,那么k＝________________

3.已知正比例函数y＝kx(k≠0),y随x的增大而减小,那么反比例函数y＝,当x＜0时y随x的增大而________________________.

4.若双曲线y＝与直线y＝x＋b无交点,则b的取范围是__________________.

5.双曲线y＝(2m＋1)x^m的两个分支分别位于第___________________象限.

6.点A在函数y＝(x＞0)的图象上，如果AH⊥x轴于H，且AH：HO＝2，那么点A的坐标是_________________.

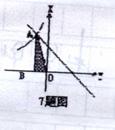
7.如图1,Rt△AOB的顶点A是一次函数y＝－x＋m＋3图象与反比例函数的图象在第二象的一个交点,且S_△AOB＝1,那点A的坐标是____________________,m＝____________________.

8.已知A(m＋3),2和B(3,)是同一个反比例函数图象上的两点,则m的值是______________.

9.反比例函数y＝的图象上有一点P(m,n),且m,n是关于t的一元二次方程t²－3t＋k＝0的两根,且P点到原点的距离为,则这个反比例函数的解析式为_________________.

10.已知点P(1,a)在反比例函数y＝(k≠0)的图象上,其中a＝m²＋2m＋3(m为实数),则这个函数的图象在第______________象限.

二、选择题(每题3分,共24分)

11.若m＜1,则下列函数①y＝;②y＝－mx＋1;③y＝－(x＞0); ④y＝(m＋1)x中,y随x增大而增大的有(　　)

A.1个　　  B.2个　　　C.3个　　　 C.4个

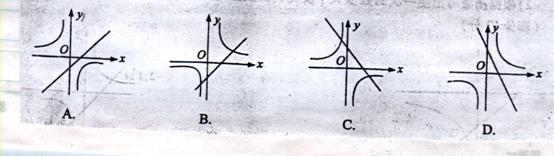
12.(多选)在同一平面直角坐标系中,如图2所示,函数 y＝k(1－k)与y＝(k≠0)的大致位置关系是(　　)

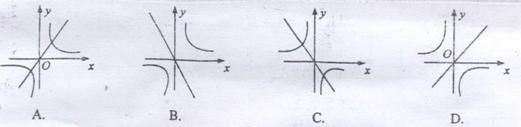
13.如图3,在同一直角坐标系中,正比例函数y＝(m－1)x与反比例函数y＝的图象的大体位置不可能是(　　)

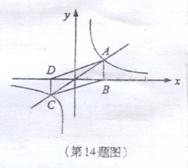
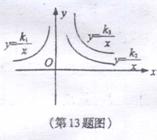
14.如图4所示是三个反比例函数y＝, y＝, y＝在x轴上方的图象,由此观察行到k₁,k₂,k₃的大小关系为(　 )

A. k₁＞k₂ ＞k₃  B. k₃＞k₂＞ k₁

C. k₂＞k₃＞k₁  D. k₃ ＞k₁＞k₂　　　　　　　　 

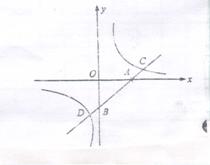
15.如图5,过原点O的直线AC交y＝(k≠0)的图象于A，C两点,AB，CD垂直于x轴,垂足分别为B，D,那么四边形ABCD的面积是(　 )

A. 　　 B.2k　　 C.4k　　　　D.k

16. 在反比例函数y＝ －的图象上有三点(x₁,y₁)　，(x₂,y₂) ，(x₃,y₃) , 若x₁＞x₂＞0＞x₃　,则下列各式正确的是(　　)

A. y₃ ＞y₁ ＞y₂  B. y₃ ＞y₂ ＞y₁

C. y₁ ＞y₂ ＞ y₃D. y₁ ＞y₃＞ y₂

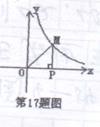17.反比例函数y＝(k＞0),在第一象限内的图象如图6,点M是图象上一点,MP垂直x轴于点P,如果△MOP的面积为1,那么K的值是(　　)

A. 1　　　B.2　　　C.4　　D.

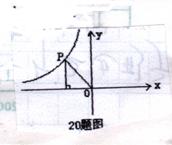18.如图7,P(a,b)在反比例函数y＝(k≠0)的图象上,且a,b是函数t²－t－12＝0的两根,过P作PA⊥x轴于点A,则△PAO的周长是(　 )

A.7　　　 B.10　　C.11　　D.12

三、解答题(共46分)

19.( 7分)面积一定的梯形其上底是下底的,设下底长为x＝15cm时,高y＝16cm.求(1)y与x的函数关系式. (2)求当y＝4cm时,上底长为多少?

20. ( 7分)已知变量y与x成反比例,并且当x＝2时,y＝－3,

(1)求y与x的之间的函数关系式;

(2)求当y＝2时,x的值;

(3)在直角坐标系中画出(1)小题中的函数图象的草图.

21. (８分)如图8一次函数y＝kx＋b的图象与反比例函数y＝的图象交于A,B两点.

(1)利用图中条件求反比例函数和一次函数的解析式;

(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.

22. (８分)已知关于X的方程x²－4x＋2t＝0有两个实数根.

(1)求t的取值范围.

(2)设方程的两个根的倒数和为S,求S与t之间函数关系式.

(3)在下所给的直角坐标系内,直接画出(2)中所得到的函数图象.

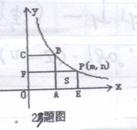23. (８分)如图9,已知正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C在y轴上,点B在函数y＝(k＞0,x＞0)的图象上,点P(m,n)是函数y＝kx(k＞0, x＞0)的图象上任意一点,过P分别x轴,y轴的垂组,垂足分别为E,F,并设矩形OEPF与正方形OABC不重合部分的面积为2.

(1)求B的坐标和K的值.

(2)当S＝时,求点P的坐标.

(3)写出S关于m的函数关系式.

24. (８分)如图10,一次函数的图象与x轴，y轴交于A，B两点，与反比例函数的图象交于C，D两点.如果A点的坐标为（2，0），点C，D分别在第一，三象限，且OA，OB＝AC＝BD，试求一次函数与反比例函数的解析式.

答案

一、1.m＞1　　　 2. m＝－1　　　3.增大　　  4.－2＜b＜2　　 5.二,四　　6.((2)或(－2))　  7.A的坐标为(－1,2), m＝－2　　 8. m＝－6　 9.y＝－　10.一,三象限　

二、11.A　  12.AD　　13.B　 14.B　 15.A　　 16.D　 17.B　 18.D　　

三、19.(1)y＝　  (2)7.5cm　　  20.(1) )y＝　 (2)x＝－3　　(3)略　　 21.(1) y＝－, y＝x－1　　(2)当x＜1－2或0 ＜x＜1时,一次函数的值大于反比例函数值　　22.(1)依题意△≥0,即(－4)²－8t≥0　　∴t≤2　　(2)设方程的两根为x₁,x₂,且x₁ ·x₂,≠0则x₁＋x₂＝4　x₁×x₂,＝2t　S＝(t≤2且t≠0)　 (3)略

23.(1)B点的坐标为(3,3)　　 k＝9　　 (2)P₁＝(6,)P₂(,6)　  (3)S＝9－3m(0＜

m＜3)　 S＝9－(m≥3)　　24.y＝x－2,y＝