八年级数学第二学期期中模拟卷
一、选择题（给出的四个选项中只有一个是正确的，把你认为正确的答案代号填在相的小括号内，每小题3分，共15分）
1、在中分式的个数有（ ）
A、2个 B、3个 C、4个 D、5个
2、要使分式有意义，则x应满足 （ ）
A、x≠-1 B、x≠2 C、x≠±1 D、x≠-1且x≠2
3、如果把分式中的x和y都扩大2倍，即分式的值（ ）
A、扩大4倍； B、扩大2倍； C、不变； D缩小2倍
4、下列关系式中，y是x反比例函数的是（ ）
A、 B、 C、 D、
5、如图，函数
的图象是下图的（ ）
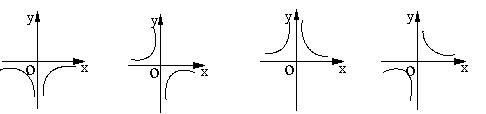
A B C D
二、填空题（每小题3分，共30分，请把下列各题的正确答案填在横线上）
6、计算：—6—1=_______.
7、用科学记数法表示：—0.=______________.
8、当x =______时，分式 的值为零.
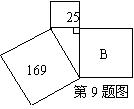9、如图字母B所代表的正方形的面积是：_______.
10、反比例函数的图象经过点（3，4），则它的解析式是__________.
11、直角三角形两直角边分别为6cm,8cm，那么这个直角三角形的斜边长为：_______cm.
12、已知点A（2，y1），B（1，y2）在反比例函数y= (k 0)的图象上，则y1___y2.
13、 在Rt△ABC中，∠C=90°,∠C的对边为c, c=7,b=3, 则a=_______.
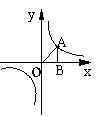
14、已知如图，点A是反比例函数y= 图象上任一点，
AB垂直x轴于点B，则△AOB面积是________.
15、一份工作，甲单独做需a天完成，乙单独做需b天完成，
则甲乙两人合作一天的工作量是________.
三、解答题（每小题5分，共30分）
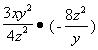
16、计算：
17、计算：
18、计算：
19、计算：
20、解方程：
21、解方程：
四、化简求值：（每小题3分，共6分）
22、（1）先化简（2）再求值
，其中
五、解答题（23题至26题每小题6分，27题7分，28题8分，共39分）
23、已知反比例函数的图象过点A（-2，4）。
（1）这个函数的图象分布在哪些象限？y随x的增大如何变化？
（2）点B（4，-2）、C（6，
）、D（1，8）是否在这个函数的图象上？
24、某校八年级学生到离校15千米的山坡植树，一部分学生骑自行车，先出发
小时，其余学生乘汽车出发，结果同时到达，汽车速度是自行车速度的3倍，求自行车、汽车的速度各是多少？
25、某空调厂的装配车间计划组装9000台空调：
（1）从组装空调开始，每天组装的台数m（单位：台/天）与生产的 时间t（单位：天）之间有怎样的函数关系？
（2）原计划用2个月的时间（每月以30天计算）完成，由于气温提前升高，厂家决定这批空调提前十天上市，那么装配车间每天至少要组装多少空调？
26、小东拿着一根长竹秆进一个宽为3米的城门，他先横着拿不进去，又竖起来拿，结果秆比城门高1米，当他把秆斜着时，两端刚好顶着城门的对角，问秆长多少米？
27、请阅读下列解题过程：已知a、b、c、为△ABC的三边，且满足
试判断△ABC的形状。
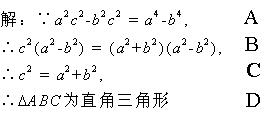
问：
(1) 在上述解题过程中，从哪一步开始出现错误：_______________.
(2)错误的原因是：_________________.
(3)本题正确的结论是 ：__________________________.
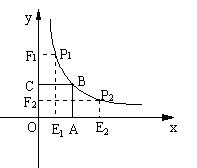28、如图，正方形OABC的面积为9，点O为坐标原点，点B在函数y=
(k>0,x>0)的图象上，点P（m, n）是函数y= (k>0,x>0)的图象上任意一点，过点P分别作x轴、y轴的垂线，垂足分别为E、F，并设矩形OEPF和正方形OABC不重合部分的面积为S。（提示：考虑点P在点B的左侧或右侧两种情况）
（1）求B点坐标和k的值；
（2）当S= 
时，求点P的坐标；
（3）写出S与m的函数关系式。