平行四边形单元测试题
一、填空题
1、□ABCD中，∠A和∠B是一对邻角，如果∠A︰∠B=4︰5，那么∠A=_____，∠D=________.
2、一个菱形的边长与一个等腰直角三角形的直角边长相等，若菱形的一个内角为30°，则菱形的面积与等腰直角三角形的面积之比为________.
3、以线段a=16，b=13为梯形的两底，c=10为一腰，那么另一腰d的长度范围是________.
4、如图，若将正方形分成k个完全一样的矩形，其中上、下各横排两个，中间竖排若干个，则k=________.
5、已知：矩形ABCD中，CE⊥BD，E为垂足，∠BCE︰∠ECD=3︰1，那么∠ACE=________度.
二、选择题
6、如图，□ABCD的对角线AC，BD相交于点O，EF过点O，与AD、BC分别相交于点E、F，如果AB=4，BC=5，OE=1.5，则四边形EFCD的周长为
（ ）
A．16 B．14 C．12 D．10
7、能够找到一点，使该点到各顶点的距离都相等的图形是（ ）
①平行四边形 ②菱形 ③矩形 ④正方形
A．①与② B．②与③ C．②与④ D．③与④
8、等腰梯形ABCD中，对角线AC=BC＋AD，则∠DCB的度数是（ ）
A．30° B．45° C．60° D．90°
9、下面的图形中，既是轴对称图形，又是中心对称图形的是（ ）
A．角 B．任意三角形 C．矩形 D．等腰三角形
10、已知直角梯形的一条腰长为5厘米，这腰与底边成30°的角，则这梯形另一腰的长为（ ）
A．10厘米 B．5厘米
C．2.5厘米
D．7.5厘米
11、如图矩形ABCD沿AE折叠，使D点落在BC边上的F点处，如果∠BAF=60°，则∠DAE等于（ ）
A．15° B．30° C．45° D．60°
12、已知一个四边形ABCD的边长分别是a，b，c，d，其中a，c为对边，且a2＋b2＋c2＋d2=2ac＋2bd，则此四边形是（ ）
A．任意四边形 B．对角线互相垂直的四边形 C．平行四边形 D．对角线相等的四边形
13、如图，正方形ABCD中，CE⊥MN，∠MCE=40°，则∠ANM=（
）
A．40° B．45° C．50° D．55°
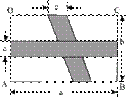14、如图，在矩形ABCD中，横向阴影部分是矩形，另一阴影部分是平行四边形，根据图中标注的数据，计算图中空白部分的面积，其面积是（
）
A．ac＋bc－ab＋c2 B．ab－bc－ac＋c2 C．a2＋ab＋bc－ac D．b2－bc＋a2－ab
15、下图四个图形中，既是轴对称图形又是中心对称图形的是（ ）
A．（1）（2）（3）（4） B．（1）（2）（3） C．（1）（3） D．（3）
三、解答题
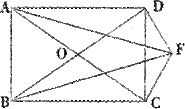16、如图，若F为矩形ABCD外一点，且∠BFD=90°，求证：∠AFC=90°.
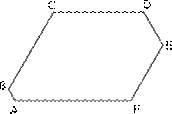
17、如图已知六边形ABCDEF的每一个内角都是120°，且AB=1，BC=CD=7，DE=3，求这个六边形的周长。
18、印刷一张矩形广告（如图），它的印刷面积为32平方分米，上下空白各1分米，两边空白各0.5分米，设印刷部分从上到下的长为x分米，四周空白处的面积为S平方分米。
（1） 写出S与x的关系式.
（2）当要求四周空白处的面积为18平方分米时，求用来印刷这张广告的纸张的长和宽各是多少？
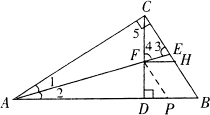
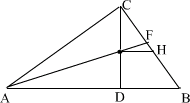19、如图，Rt△ABC中，∠ACB=90°，CD⊥AB于D，AE平分∠CAB交CD于F，求BC于E，过F作FH∥AB，交BC于H.
求证： CE=BH.
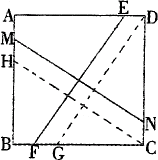
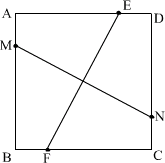20、已知，如图所示，正方形ABCD，E、M、F、N分别是AD、AB、BC、CD上的点，若EF⊥MN，求证：EF=MN.
参考答案
一 1 、 80° ， 100°
提示：利用邻角互补求解 .
2 、 1 ︰ 1
提示：设菱形边长为 x ，则面积:
∴比为 1 ︰ 1.
3 、 7<d<13
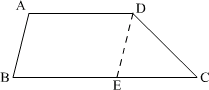
提示：如图，过 D 作 DE ∥ AB ，在△ DEC 中，可知 10 － 3<d<10 ＋ 3 ，
即 7<d<13.
4 、 8
5 、 45
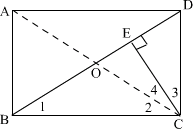
提示：如图，连结 AC ，交 BD 于点 O ，则 OB=OC.
由∠3 ＋∠2 ＋∠4=90 °，且∠3 ︰（∠2 ＋∠4 ） =1 ︰ 3
可知∠3= ∠2= ∠1=22.5 °，∴ ∠4=2 × 22.5 ° =45 ° .
6 、 C 7 、 D 8 、 C 9 、 C 10 、 C
11 、A 12 、C 13 、C 14 、B 15 、D
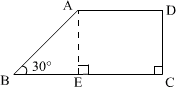10 、 提示：如图，过 A 作 AE ∥ DC ，在 Rt△ABE 中易求
，
∴ 选 C 。
11 、
提示：易知△ ADE ≌△ AFE ，∴ ∠DAE= ∠FAE
∠DEA= ∠FEA ，∵ ∠BAF=60°，易知∠AFB= ∠FEC=30°
∴ ∠DEF=180°－ 30° =150°，故∠AED=75°
∴ ∠DAE=15° .
13 、
提示：由∠BCE=45°，可知∠CEB=50° .
∴ ∠AEC=130°，又∠NAE=90°， MN ⊥ EC ，垂足设为 O.
则∠EON=90°，易知∠ANO=180°－ 130° =50° .
14 、
提示：∵ S□=bc ， S矩形 =ac ，又重叠部分的面积为 c2 ，∴ 应选 B 。
16 连结 OF ，在 Rt△BDF 中， OF 为斜边 BD 上的中线， OF=
BD
，所以 OF=AC
，即 OA=OC=OF ，从而可证得∠AFC=90
°。
17 解：如图，延长 FA 、 CB 相交于 G 点，延长 CD 、 FE 相交于 H 点，
由条件可知：
△ABG 和△EDH 都是等边三角形 .
∴ ∠G= ∠H=60 °
∴ 四边形 CGFH 是平行四边形
∴ GF=CH=CD ＋ DH=CD ＋ DE=7 ＋ 3=10
∴ AF=GF － AG=GF － AB=10 － 1=9
同理 FE=5
∴ 六边形的周长为 1 ＋ 7 ＋ 7 ＋ 3 ＋ 9 ＋ 5=32
18 解：（1）设印刷部分长为 x 分米，于是其宽为
分米，进而广告纸宽为
.
∴ 空白部分面积
.
这就是 S 与 x 的关系式 .
（2）当 S=18dm2 时，有
，整理得 (x － 8)2=0
， x=8.
∴ 广告纸的长为 x＋2=10(dm) ，宽为＋ 1=5(dm)
19 证明：过 F 作 FP ∥ BC 交 AB 于 P ，则四边形 FPBH 为平行四边形 .
∴∠B=∠FPA.BH=FP
（平行四边形对边相等）
∵∠ACB=90 °， CD ⊥ AB.
∴∠5 ＋∠ CAB=90 °，∠ B ＋∠ CAB=90 ° .
∴∠5=∠B ，∴∠5=∠FPA.
又∵∠1=∠2 ， AF=AF.
∴ △ CAF ≌△ PAF.
∴ CF=FP ，∵∠4=∠1 ＋∠ 5 ，∠ 3=∠2 ＋∠ B,
∴∠3=∠4
∴ CF=CE ，∴ CE=BH.
20 证明：作 DG∥EF 交 BC 于 G ，作 CH∥MN 交 AB 于 H.
∵ CH∥MN ， DG∥EF ， FE ⊥ MN
∴ CH ⊥ DG ，又 ∵ DC ⊥ BC
∴∠BCH=∠CDG ，∵ BC=CD ，∠ HBC=∠GCD
∴ △DCG 按顺时针旋转 90° 后再向左平移 .
BC 的长可与△ CBH 重合 .
∴ CH=DG ，又∵ AD∥BC,DG∥EF
∴ 四边形 EFGD 为平行四边形，∴ EF=DG ，
同理 CH=MN ，∴ MN=EF.