2005学年锦绣实验学校八年级（下）数学期中练习卷
2006/04/28
班级 姓名 学号
亲爱的同学们，准备好了吗？我们相信，凭着你的自信、沉着、智慧和对数学的喜爱，一定能交上一份满意的答卷！
一、填一填：（每题2分，共20分）
1.平方根等于它本身的数是 ，64的立方根是 .
2.函数y=
中自变量x的取值范围是 .
3.任意写出一个图象经过二、四象限的反比例函数的解析式:___ ____.
4.函数y=4x-3的图象与x轴的交点是 ,与y轴的交点是 .
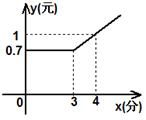5.如图，表示在某公用电话亭打电话时，需付电话费y（元）与通话时间x（分钟）之间的函数关系，如果小明付了2.2元的通话费，那么他的通话时间是 分.
|
=
，△ABC的面积为2㎝2，则△A′B′C′的面积为
㎝2.
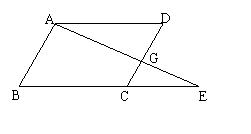
7．如图，点E是䖡ABCD的边BC延长线上的一点，AE与CD相交于点G，AC是䖡ABCD的对角线，则图中相似三角形共有
对.
|
|
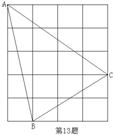
8. 如图，正方形网格中，每个小正方形的边长为1，则网格上的三角形ABC中，边长为无理数的边有 条.
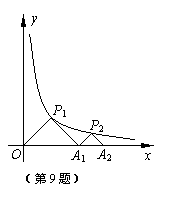
9．如图，△P1OA1、△P2 A1A2、是等腰直角三角形，
点P1 、P2在函数y＝
（x＞０）的图象上，斜边
O A1、、A1A2都在x轴上，则点A2的坐标是 .
10 .在△ABC中，∠B＝25°，AD是BC边上的高，
并且
，则∠BCA的度数为 ______ .
二、选一选：（每小题都只有一个选项正确，每小题2分，共20分）．
11.在实数
、
、0、
、
、
、
、
、2.1 ……中，无理数的个数（ ）
A、2个 B 3个 C 4个 D、5个
12.下列计算正确的是（ ）
A、
＝±3 B、（3
）
＝6 C、
D、
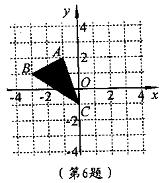
13．如图，若将△ABC绕点C顺时针旋转90°后得到△
，则点A的对应点
的坐标是（ ）
A、（－3，－2） B、（2，2）
C、（3，0） D 、（2，1）
14.下列两个图形相似的是（ ）
A、
|
C、两个等边三角形 D、两个直角三角形
15.依据下列各组条件，不能判定△ABC∽△A＇B＇C＇的是（ ）
A．∠A＝800，∠C＝600，∠A＇＝800，∠C＇＝600
B． AB＝2，BC＝3，AC＝4，A′B′＝4，B′C′＝6，A′C′＝8
C．∠A＝400，AB＝2，AC＝3，∠A＇＝400，A′B′＝4，A′C′＝6
D．∠A＝400，∠B＝600，∠A＇＝400，∠C＇＝700
16.小明骑自行车上学，开始以正常速度匀速行驶，但行至中途自行车出了故障，只好停下来修车。车修好后，因怕耽误上课，他比修车前加快了骑车速度匀速行驶。下面是行驶路程s(米)关于时间（t 分）的函数图像，那么符合这个同学行驶情况的图象大致是 （ ）
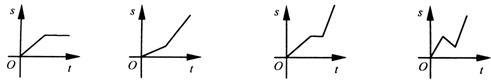
A B C D
17．直线y=－x＋2与直线y=2x－3的交点在（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
18.在平面直角坐标系中，顺次连结点（2，3）、（-2，3）、（-4，-2）、（4，-2）的四边形（ ）
A 、有一个角是直角的四边形 B 、等腰梯形
C 、对角线不相等的四边形 D 、平行四边形
|
的图象上任取点A，过A点作AB⊥x轴，交x轴于B点，则△A OB的面积是（ ）
A、1 B、2 C、4 D、8
20、一束光线从点A（3，3）出发，经过ｙ轴上点Ｃ反射后经过点
B（1，0），则光线从A点到B点经过的路线长是（ ）
Ａ、5 Ｂ、6 C、7
D、8
三、练一练：（第21题共10分，第22、23题每题7分，24、25题每题6分，26题共6分，27 题共8分）
21.（1）计算:
-
-2
+
（2）计算：
+
×
22.化简下列各式
（1）（1+
）（1-） （2）
-(
)2
23.若反比例函数y=
与一次函数
的图象都经过点A（
，2）
（1）求点A的坐标；
（2）求一次函数的解析式；
（3）设O为坐标原点，若一次函数图象与y轴的交点为B，求△AOB的面积。
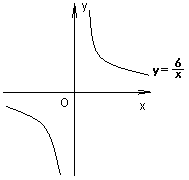
24.已知：如图，D、E是△ABC的边AB、AC上的点，AD=5，AE=4，BD=3，EC=6
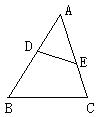∠AED＝60°，则∠B=∠AED，为什么?
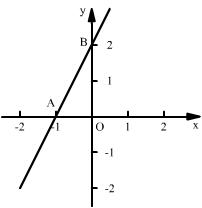25 直线y=2x+2 与x轴、y轴分别相交于A、B两点，将△AOB绕点O顺时针旋转90°，得到△A1OB1.
(1)在图中画出△A1OB1，求A1、B1的坐标。
(2)求过A1、B1两点直线解析式。
【解】
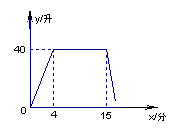
26．某洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续过程，
其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关
系如折线图所示：
根据图象解答下列问题：
（1） 衣机的进水时间是多少分钟？清洗时洗衣机中的水量是多少升？
（2） 知洗衣机的排水速度为每分钟19升，
① 排水时y与x之间的关系式。
②如果排水时间为2分钟，求排水结束时洗衣机中剩下的水量。
 |
27 如图，已知平面直角坐标系中三点A（2，0），B（0，2），P（x，0）
，连结BP，过P点作
交过点A的直线a于点C（2，y）
（1）求y与x之间的函数关系式；
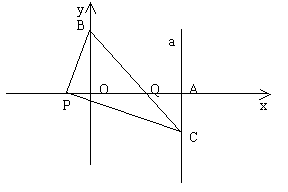（2）当x取最大整数时，求BC与PA的交点Q的坐标。
附加题（分值记入总分，但总分不超过100分，28题3分，29题7分）
28． 如图，把矩形OABC放置在直角坐标系中，OA＝6，OC＝8，若将矩形折叠，使点B与O重合，得到折痕EF。
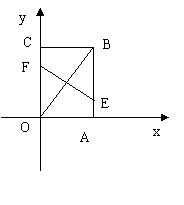（1）可以通过 _办法，使四边形AEFO变到四边形BEFC的位置（填“平移”、“旋转”或“翻转”）；
（2）求点E的坐标 ；
（3） 若直线l把矩形OABC的面积分成相等的两
部分，则直线l必经过点的坐标是 __.
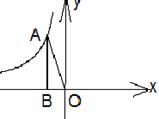
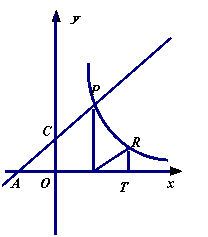
29. 如图，直线y=x+2分别交于x, y轴于点A、C，P是该直线上在第一象限内的一点，PB⊥x轴，垂足为B， S△ABP＝9
⑴求点P的坐标；
⑵设点R与点P在同一反比例函数的图象上，且点R在直线PB的右侧，作RT⊥x轴，T为垂足，当△BRT与△AOC相似时，求点R的坐标。
|