初二数学（下）期中试题
一、选择题（每题２分，共30分）
1、下列说法正确的是（ ）
A、任何数的平方根都有两个。 B、 只有正数才有平方根
C、一个数的平方的平方根就是这个数。 D、一个正数的平方根的平方就是这个数
2、．在下列长度的四根木棒中，能与
（A）
3、下列结论：①在数轴上只能表示无理数；②任何一个无理数都能用数轴上的点来表示；
③实数与数轴上的点一 一对应；④有理数有无限个，无理数有有限个。其中正确的是（ ）
A、①② B、②③ C、③④ D、②③④
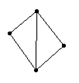
4、下列由几根木条用钉子钉成如下的模型，其中在同一平面内不具有稳定性的是（ ）
 | |||||||
 | |||||||
 |  | ||||||
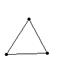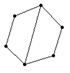A B C D
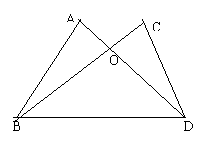
5、如图，AB=CD，AD=BC，AC和BD交于点M，那么图中全等三角形有 （ ）
A、2对 B、3对 C、4对 D、5对
6、在下图中，正确画出AC边上高的是（ ）．
 |
（A） （B） （C） （D）
7、已知ΔABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=2∠A，则此三角（ ）
A、一定有一个内角为45° B．一定有一个内角为60°
C．一定是直角三角形 D．一定是钝角三角形
8、下列说法：①带根号的数都是无理数；②不带根号的数都是有理数；③无理数一定是无限不循环小数；④无限小数不一定是无理数，其中正确的有( )
A．1个 B．2个 C．3个 D．4个
9、下列说法不正确的是 ( )
A．±6是36的平方根； B．6是36的一个平方根；
C．36的平方根是6； D．36的平方根是±6
10、在实数0、3、
、
、π、
、
中无理数的个数是 ( )
A．1 B．
11、在△ABC和△A'B'C'中 , ①AB=A'B' , ②BC=B'C' , ③AC=A'C , ④∠A=∠A' , ⑤∠B=∠B' , ⑥∠C=∠C' , 则下列哪组条件不保证△ABC≌△A'B'C'． （ ）
A、①、②、③ B、①、②、⑤ C、①、⑤、⑥ D、①、②、④
12、如图，某人不小心把一块三角形的玻璃打碎成三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是 （ ）
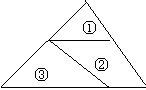A 、带①去
B 、 带②去
C 、 带③去 D 、带①和②去
13、在下列条件中：①∠A+∠B=∠C， ②∠A∶∠B∶∠C=1∶2∶3， ③∠A=900－∠B， ④∠A=∠B=∠C中，⑤∠A=2∠B=3∠C能确定△ABC是直角三角形的条件有（ ）
A、5个 B、2个 C、3个 D、4个
14、下列判断①-512的立方根是-8 ②-1331的三次算术根是-11 ③
的算术平方根是
④正数a的三次方根是±
其中正确的有（ ）个。
A、1个 B、2个 C、3个 D、4个
15、现有四个无理数：
、
、
、
，其中在实数
+1与
+1之 间的有( )
A．1个 B．2个 C．3个 D．4个
二、填空：（每题3分，共30分）
1、
的平方根是 。
2、某位同学的卧室有16平方米，共用了64块正方形的
地板砖，则每块地板砖的边长是 米。 4题图
3、直角三角形两个锐角的平分线所构成的钝角等于_____ 度。
4、如图，已知∠A =∠C，要证明⊿AOB≌⊿COD,根据“ASA”还要一个条件__________。
5、实数
满足
则是
。
6、若等腰三角形两边长分别是4cm、5cm, 则这个三角形的周长是 .
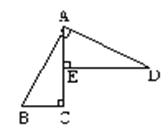
7、已知：如图 , AC⊥BC于C , DE⊥AC于E ,
AD⊥AB于A , BC=AE．若AB=5 , 则AD=___________．
8、写出一个大于2而小于5的无理数 。
9、AD是⊿ABC的中线。⊿ABD的周长比⊿ADC的周长大4，
则AB 与 AC的差为_________。
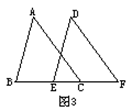
10、已知：如图3，∠ABC＝∠DEF，AB＝DE，要说明△ABC≌△DEF，
（1）若以“SAS”为依据，还须添加的一个条件为 ；
（2）若以“ASA”为依据，还须添加的一个条件为 ；
（3）若以“AAS”为依据，还须添加的一个条件为 ；
三、解答题：（共２５分）
1、（5分）实数a、b、c、在数轴上的位置如图所示，
化简： 
2、（6分）如图，直线AC∥DF，C、E分别在AB、DF上，小华想知道∠ACE和∠DEC是否互补，但是他有没有带量角器，只带了一副三角板，于是他想了这样一个办法：首先连结CF，再找出CF的中点O，然后连结EO并延长EO和直线AB相交于点B，经过测量，他发现EO＝BO，因此他得出结论：∠ACE和∠DEC互补，而且他还发现BC＝EF。以下是他的想法，请你填上根据。
小华是这样想的：
因为CF和BE相交于点O，
根据 得出∠COB＝∠EOF；
而O是CF的中点，那么CO＝FO，又已知 EO＝BO，
根据 得出⊿COB≌⊿FOE，
根据 得出BC＝EF，
根据 得出∠BCO＝∠F，
既然∠BCO＝∠F，根据 出AB∥DF，
既然AB∥DF，根据 得出∠ACE和∠DEC互补。
3、（5分）已知： 2x+1的平方根是±5，求5x+4的立方根。
4、（5分）如图AB、CD相交于点O，AO＝BO，AC∥DB。那么OC与OD相等吗？说明你的理由
 |
5、（4分）如图，有一块三角形的土地，现在要求过三角形的某个顶点画一条线段，将它的面积平均分
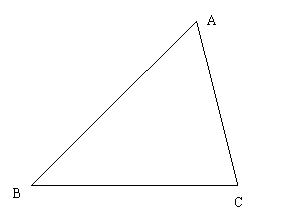成两份，你认为这条线段应该如何画？在图中画出；简要说明为什么。
6、（６分）已知：图中，∠B=40°，∠C=60°，AD、AF分别是△ABC的角平分线和高（6分）
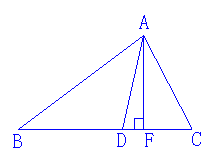（1）∠BAC等于多少度？
（2）∠DAF等于多少度？
四、证明题：
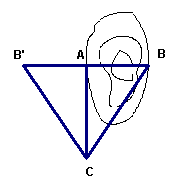
1、（６分）已知如图，要测量水池的宽AB，可过点A作直线AC⊥AB，再由点C观测，在BA延
长线上找一点B’，使∠ACB’= ∠AC B，这时只要量出A’B’的长，就知道AB的长， 对吗？为什
么？ 你还有其它想法吗？请在右图中画出你所想的图形。不用说明为什么 。
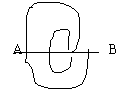
2、（６分）如图6，已知∠1=∠2，∠3=∠4，
求证：AB=CD
五、探索题：1、（７分）（1）如图1，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C．△ABC中，∠A＝30°，则∠ABC＋∠ACB＝ 度，∠XBC＋∠XCB＝ 度；
（2）如图2，改变直角三角板XYZ的位置，使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C，那么∠ABX＋∠ACX的大小是否变化？若变化，请举例说明；若不变化，请求出∠ABX＋∠ACX的大小．
 |
2、（１０分）（1）如图1，AC、BD交于点E，给出怎样的两个条件，可以说明△ADE≌△BCE？为什么？
（2）如图2，在△ABC与△BAD中，给出怎样的两个条件，可以说明△ACE≌△BDE？为什么？
 |
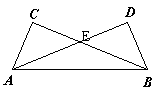答案：一、1、D、2、C、3、B、4、C、5、C、6、C、7、B、8、B、9、C、10、B、11、D、12、D、13、D、14、A、15、B
二、填空：±2、2、
、3、135°、4、OA=OC、5、非正数、6、15或13厘米、7、5、8、
9、4、10、①BC=EF ②∠A=∠D ③∠ACB=∠F
三、1、c-b 2、略
