2005学年八年级(下)高桥镇三校期中联考数学试题2006.4.
(答题时间:90分钟,满分100分) 命题学校:南日初中
亲爱的同学:数学使人严谨,数学使人聪明,数学充满趣味,你对数学感兴趣吗?通过前一段时间的努力,到了展示你的数学能力的时候了,祝你成功!
一、认真填一填(每题3分,共30分)
1、已知a<b,用“<”或“>”号填空: ![]() ▲
▲ ![]()
2、某月日历一横排上连续三个数字之和小于11,则这三个数可能是 ▲
 3、计算: 2006×
3、计算: 2006×![]() = ▲ 。
= ▲ 。
4、计算: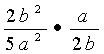 = ▲ 。
= ▲ 。
5、若分式![]() 的值为零,则x = ▲ 。
的值为零,则x = ▲ 。
 6、多项式x2+kx+9是完全平方式,那么k
= ▲ 。(只要写出一个符合要求的K值即可)
6、多项式x2+kx+9是完全平方式,那么k
= ▲ 。(只要写出一个符合要求的K值即可)
![]() 7、
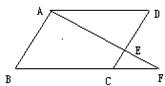
7、![]() 已知: ABCD, A、E、F共线,B、C、F共线,
已知: ABCD, A、E、F共线,B、C、F共线,
则(1)与△FCE相似的三角形有 ▲ 对
(2)若CE=1,ED =2, CF=2。则BC长 ▲ (第7题)
 8、沪杭磁悬浮列车工程将在今年底开工,现在比例尺是1∶的《中国政区》地图上,量得杭州与上海之间的距离为2.5厘米,那么该工程的直线距离(杭州与上海实际距离)是 ▲ 千米.
8、沪杭磁悬浮列车工程将在今年底开工,现在比例尺是1∶的《中国政区》地图上,量得杭州与上海之间的距离为2.5厘米,那么该工程的直线距离(杭州与上海实际距离)是 ▲ 千米.
9、若![]() , 则
, 则![]() ▲ ;
▲ ;
10、电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,若舞台AB长为20m,试计算主持人应走到离A点至少 ▲ m处?(结果精确到0.1m)
二、仔细选一选(每题3分,共30分)
11、下列代数式中,不是分式的是 ……………………………………( ▲ )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、如图,用不等式表示数轴上所示的解集,正确的是……………… ( ▲ )
 |
A、x<-1或x≥-3 B、x≤-1或x>3 C、-1≤x<3 D、-1<x≤3
13、下列各式中,不能分解因式的有 ………………………………( ▲ )
①
![]() ; ②
; ② ![]() ; ③
; ③![]() ;
;
④![]() ; ⑤
; ⑤ ![]() ; ⑥
; ⑥ ![]()
A. 2个 B. 1个 C. 3个 D. 4个
14、以下两个图形必定相似的是…………………………………………( ▲ )
A、有两条边对应成比例的等腰三角形 B、有一角是![]() 的等腰三角形
的等腰三角形
C、有一个角是![]() 的等腰三角形 D、有一个角相等,两边成比例的三角形
的等腰三角形 D、有一个角相等,两边成比例的三角形
15. 若关于x的方程![]() 产生增根,则m是……………………( ▲ )
产生增根,则m是……………………( ▲ )
A.-1 B.1 C.-2 D.2
16、两个相似菱形边长之比为1:4,则他们的面积比为………………( ▲ )
A 1:2 B 1:4 C 1:8 D 1:16
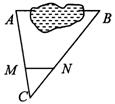
17、如图,A、B两点被池塘隔开,在AB外任选一点C,连结AC、BC分别取其三等分点M、N量得 MN=38m.则AB的长是……………………( ▲ )
A. 152m
B.114m C.76m D.104m
 (第17题)
(第17题) 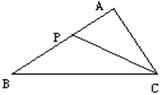 (第18题)
(第18题)
18、如图,△ABC中,P为AB上一点,下列四个条件中(1)∠ACP=∠B
(2)∠APC=∠ACB (3)AC2=AP•AB (4)AB•CP=AP•CB
能满足△APC和△ACB相似的条件是………………( ▲ )
A (1)(2)(4) B (1)(3)(4) C (2)(3)(4) D (1)(2)(3)
19、设“●”、“▲”、“■”表示三种不同的物体.现用天平称两次,情况如图所示,
那么●、▲、■这三种物体质量从大到小的顺序排列正确的是………( ▲ )
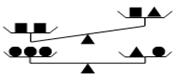
(A) ■、●、▲ (B)■、▲、●
(C)▲、●、■ (D)▲、■、●
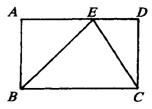 20、如图,在矩形ABCD中,点E是AD上任意一点,则有 …………( ▲ )
20、如图,在矩形ABCD中,点E是AD上任意一点,则有 …………( ▲ )
A.△ABE的周长+△CDE的周长=△BCE的周长
B.△ABE的面积+△CDE的面积=△BCE的面积
C.△ABE∽△DEC D.△ABE∽△EBC

三、计算题(共40分)
21、解不等式组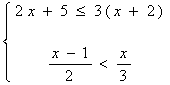 把它的解表示在数轴上,并写出不等式组的整数解.
(共6分)
把它的解表示在数轴上,并写出不等式组的整数解.
(共6分)
22、把下列各式分解因式(每小题3分,共6分)
(1)a2 –9 (2)x2y – 4xy2 +4 y3
23、解分式方程(本题5分) 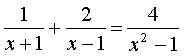
24、先化简再求值(注意:两小题任意选做一题,以其中一小题计得分,5分)
①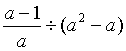 ,其中a=-1 ②
,其中a=-1 ②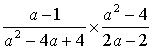 ,其中a=-1
,其中a=-1
25、应用题:南日初中餐厅在2006年4月计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元.甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售.那么,什么情况下到甲商场购买更优惠?(8分)
26、已知:△ABC中,AB=5,AC=4,BC=3,PQAB,P在AC上(与A,C不重合),Q在BC上。(1)当△PQC的面积与四边形PABQ的面积相等时,求CP的长。
(2)当△PQC的周长与四边形PABQ的周长相等时,求CP的长。
(3)试问:在AB上是否存在点M,使得△PQM为等腰三角形?若存在,请求出PQ的长;若不存在,请简要说明理由。(本题10分)
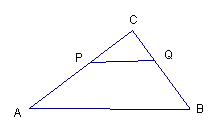
(第26题图)
四、附加题:5分,计入总分但总分不超100分
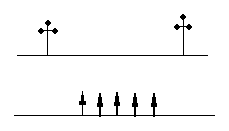 一条河的两岸有一段是平行的.在河的这一岸每相距5米在一棵树,在河的对岸每相距50米在一根电线杆.在这岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽.(在示意图上构造数学图形并写出解答过程)
一条河的两岸有一段是平行的.在河的这一岸每相距5米在一棵树,在河的对岸每相距50米在一根电线杆.在这岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽.(在示意图上构造数学图形并写出解答过程)
| 题 号 | 一(30分) | 二(30分) | 三(40分) | 附加题 (5分) | 总分 (100分) |
| 得 分 |
![]()
 2005学年八年级(下)高桥镇三校期中联考数学答题卷
2005学年八年级(下)高桥镇三校期中联考数学答题卷
一、认真填一填(每题3分,共30分)
1、 ; 2、 ;
3、 ; 4、 ;
5、 ; 6、 ;
7、 、 ; 8、 ; 9、 ; 10、 。二、仔细选一选(每题3分,共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
三、计算题(共40分)
21、解不等式组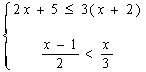 把它的解表示在数轴上,
把它的解表示在数轴上,
并写出不等式组的整数解. (共6分)
22、把下列各式分解因式(每小题3分,共6分)
(1)a2 –9 (2)x2y – 4xy2 +4 y3
23、解分式方程(本题5分) 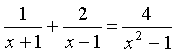
24、先化简再求值(注意:两小题任意选做一题,以其中一小题计得分,5分)
①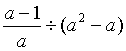 ,其中a=-1 ②
,其中a=-1 ②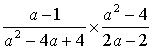 ,其中a=-1
,其中a=-1
25、(本题8分)
26、已知:△ABC中,AB=5,AC=4,BC=3,PQAB,P在AC上(与A,C不重合),Q在BC上。(1)当△PQC的面积与四边形PABQ的面积相等时,求CP的长。
(2)当△PQC的周长与四边形PABQ的周长相等时,求CP的长。
(3)试问:在AB上是否存在点M,使得△PQM为等腰三角形?若存在,请求出PQ的长;若不存在,请简要说明理由。(本题10分)

四、附加题:(本题5分,计入总分但总分不超100分)
一条河的两岸有一段是平行的.在河的这一岸每相距5米在一棵树,在河的对岸每相距50米在一根电线杆.在这岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽.(在示意图上构造数学图形并写出解答过程)
 |