2005学年第二学期天河中学期中水平测试卷
八年级数学
(时间120分钟，满分100分)
| 题 号 | 一 | 二 | 三 | 总 分 | ||||||||
| 23 | 24 | 25 | 26 | 27 | 28 | |||||||
| ① | ② | ③ | ④ | |||||||||
| 得 分 |
|
|
|
|
|
|
|
|
|
|
|
|
一、填空题：（每题2分，共24分）
1、81的平方根是 ，
的立方根是
。
2、若函数
中自变量x的取值范围是 。
3、用计算器计算
（精确到0.01）≈
。
4、比较大小：（1）
（2）
（填>,=,<）
5、请写出一个
的同类二次根式： 。
6、点A（2，－3）关于x轴对称的点的坐标为_________。
7、双曲线
，经过点(3，2)，则k= 。
8、正比例函数
，当m
时，y随x的增大而增大。
9、当x_______时，一次函数
的函数值大于1。
10、在ΔABC和ΔA′B′C′中，已知∠B=∠B′，要能判断这两个三角形相似，只需再加一个条件：_______________。
11、已知△ABC∽△
，两三角形最大边分别是13和26，则它们周长的比为________，面积比为__________。
|
|
|
|
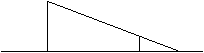
能打过网，而且落在里网4米的位置，则球拍击球的高度h为 米.
二、选择题：（每小题都只有一个选项正确，每小题3分，共30分）
| 题号 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 答案 |
13、在实数
、
、0、
、
、
、
、
、2.……（不循环）中，无理数的个数为（ ）
A、2个 B、3个 C、4个 D、5个
14、下列各式正确的是（ ）
A、=±6 B、 - =-2 C、=-6 D、=-
15、下列给出的四个点中，不在直线y=2x-3上的是（ ）
A、（1， -1） B、（0， -3） C、（2， 1） D、（-1，5）
16、在比例尺为1∶20000的地图上，量得甲、乙两地的距离为25cm，则两地的实际距离为（ ）
A、250000cm B、25km C、500km D、5km
17、当路程s一定时,速度V与时间T之间的函数关系是( )
A.正比例函数. B.反比例函数; C.一次函数. D. 以上都不是.
18、过点Ａ（0,－2）和B（2,0）两点的直线
解析式为（ ）
A、
B、
C、
D、
19、当k>0,b>0时，直线y=kx+b与双曲线y=的交点在第( )象限。
A、一、三 B、二、四 C、一、二 D、三、四
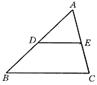
20、如图：在△ABC中，D、E两点分别在ＡＢ、ＡＣ边上，
且ＤＥ∥ＢＣ，则下列各式成立的是（ )
A、
B、
C、
D、
21、下列说法正确的个数有（ ）个
①所有的等边三角形都相似 ②有一个角相等的两个等腰三角形相似
③所有等腰直角三角形都相似 ④所有矩形都相似
A、 1 B、 2 C、 3 D、 4
22、甲、乙两人同时从A地去学校，甲骑自行车，乙步行，用S表示甲、乙离学校的路程，t表示出发后的时间，能大致反映该事件的图象（ ）
 |
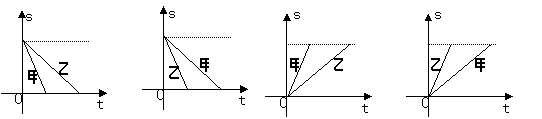A B C D
三、解答题： （共31分）
23、计算：（第①题3分，第②③题各4分，共11分）
①
；
②
；
③
；
24、（本题共6分）已知直线
经过点（1，2），且当x=
时，y=4，
求这条直线的解析式。
25、（本题共6分）已知：
，求
的平方根.
26、（本题共8分）已知直线
与x轴交于点A，直线
与x轴交于点B，且两直线交于点C。
（1） 
分别求出A、B、C三点的坐标，并画出两函数的图象。
（2） 求△ABC的面积。
四、解答题（共15分）
27、（本题共7分）已知，如图ＣＤ是直角三角形ABC斜边ＡＢ上的高，当
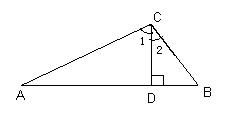ＡＤ＝１６，ＢＤ＝９时，
(1)问：△ADC∽△CDB吗？请说明理由。
(2)求：ＣＤ的长。
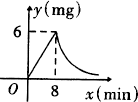28、（本题共8分）为了预防流感，某学校对教室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y(mg)与时间x(min)成正比例，药物燃烧完后，y与x成反比例（如图所示）.现测得药物8min燃毕，此时室内空气中每立方米的含药量为6mg，请根据题中所提供的信息，解答下列问题：
（1）求药物燃烧时，y关于x的函数关系式及自变量x的取值范围；
（2）求药物燃烧后，y关于x的函数关系式；
（3）研究表明，当空气中每立方米的含药量低于1.6mg时学生方可进教室，那么从消毒开始，至少需要经过多长时间，学生才能回到教室；
（4）研究表明，当空气中每立方米的含药量不低于3mg且持续时间不低于10min时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？
*第29、30题，3、7班必做题，其余班级做为附加题。
五、解答题：
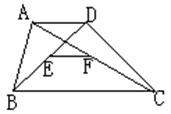29、（本题共10分）已知:如图，在梯形ＡＢＣＤ中，ＡＤ∥ＢＣ，Ｅ和Ｆ分别是对角线ＢＤ和ＡＣ中点。
求证： (1)ＥＦ∥ＢＣ
(2)ＥＦ=
(ＢＣ－ＡＤ)
30、（本题共10分）已知雅美服装厂现有A种布料70米，B种布料52米，现计划用这两种布料生产M、N两种型号的时装共80套．已知做一套M型号的时装需用A种布料1.1米，B种布料0.4米，可获利50元；做一套N型号的时装需用A种布料0.6米，B种布料0.9米，可获利45元．设生产M型号的时装套数为x，用这批布料生产两种型号的时装所获得的总利润为y元．
①求y（元）与x（套）的函数关系式，并求出自变量的取值范围；
②当M型号的时装为多少套时，能使该厂所获利润最大？最大利润是多？