2004---2005学年第二学期初二年级
期末考试数学试卷
（说明：本卷不可使用计算器；总分100分，考试时间：90分钟）
| 题号 |
一 |
二 | 三 |
总分 | |||||||||
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | ||||
| 得分 |
|
|
|
|
|
|
|
|
|
|
|
|
|
一、细心填一填:(每空2分，共30分）
1、如果2x－5＜2y－5，那么—x —y；（填“＜、＞、或＝” ）
2、分解因式：
＝
；
3、化简：
=
；
=
；
4、当x 时，分式
有意义；当m= 时，分式
的值为零；
5、若
是一个完全平方式，则k=
；
6、若2y－7x＝0，则x∶y = ；
7、已知线段AB=6cm，点C为AB的黄金分割点，且AC＞BC，则AC= ；
8、甲乙两支球队队员的平均身高都是185cm，但方差不同，
。这两支球队队员的身高较为整齐的是 ；
9、命题“垂直于同一条直线的两条直线平行”的条件是
，结论是
；
10、已知两个相似五边形的相似比为2∶3，且它们的面积
之差为15cm2 ，则较小的五边形的面积为 ；
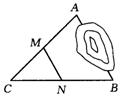
11、如右图，A、B两点被池塘隔开，在 AB外选一点 C，
连结 AC和 BC，并分别找出它们的中点 M、N．
若测得MN＝15m，则A、B两点的距离为 ；
12、一堆玩具分给x个小朋友，若每人分3件，则剩余4件； (第11题图)
若前面每人分4件，则最后一人分得的玩具不足3件。则x应满足的不等式
组为 。
二、精心选一选：（每题2分，共16分）
（注意：请将答案写在下面的表格中，否则不给分）
| 题号 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 |
13、不等式
的解集是：
A.、x≥9 B、x≤9 C、x≥
D、x≤
14、已知数据1、2、3、3、4、5，则下列关于这组数据的说法错误的是：
A、平均数、中位数和众数都是3； B、极差为4；
C、方差为10；
D、标准差是
15、为了解我校八年级800名学生期中数学考试情况，从中抽取了200名学生的数学成绩进行统计。下列判断：①这种调查方式是抽样调查；②800名学生是总体；③每名学生的数学成绩是个体；④200名学生是总体的一个样本；
其中判断正确的个数是：
A.1个 B.2个 C.3个 D.4个
16、下列各命题中，属于假命题的是：
A．若a－b＝0，则a＝b＝0 B．若a－b＞0，则a＞b
C．若a－b＜0，则a＜b D．若a－b≠0，则a≠b
17、如下图，在不等边△ABC中，若∠AED＝∠B，DE＝6，AB＝10，AE＝8，
则BC的长为：
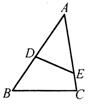A．
B．7 C．
D．
 |
O
F
(第17题图) (第18题图) (第19题图)
18、.如图，在不等边△ABC中，AB＞AC，AC≠BC，过AC上一点D作一条直线，使截得的三角形与原三角形相似，这样的直线可作（ ）条
A、2条 B、3条 C、4条 D、5条
19、如图，四边形ABDC是平行四边形，则图中有（ ）对相似三角形
A、3对 B、4对 C、5对 D、6对
20、如果
，那么k的值为：
A、-1 B、
C、2或-1 D、或-1
三、耐心解答下列各题：(共54分)
21、（4分）解不等式组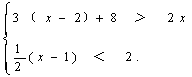
解：
22、（4分）化简求值：
其中x =
，y
=
.
解：原式=
23、（4分）解分式方程：
解：
24、（4分）把下图所示的零件缩小，使缩小后的图形各边长变为原图各边长的一半。（要求留下画图痕迹，不写画法）
 |
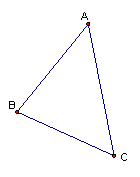25、（4分）为了了解中学生的体能情况，抽取了某中学八年级学生进行跳绳测试，将所得数据整理后，画出如图所示的频率分布直方图，已知图中从左到右前三个小组的频率分别是0.1，0.3，0.4，第一小组的频数为5。
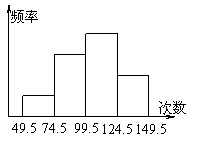(1)第四小组的频率是__________
(2)参加这次测试的学生是_________人
(3)成绩落在哪组数据范围内的人数最多？是多少？
解：
(4) 求成绩在100次以上(包括100次)的学生占测试人数的百分率.
解：
26、（5分）认真看图，你一定能发现其中的奥妙！已知：MA∥NB，
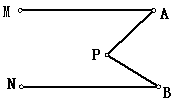
图1 图2
（1）如图1，若点P为MA、NB外部一点，此时∠P、∠A、∠B的大小有何关系？
解：
（2）如图2，若点P为MA、NB内部一点，此时∠APB与∠A、∠B的大小又有何关系？
解：
（3）请任选上面一个结论进行证明。
证明：
27、（6分）暑假学校准备组织一批学生参加夏令营，联系了甲、乙两家旅行社，他们的服务质量相同，且入营费都是每人200元。经过协商，甲旅行社表示可以给每位入营队员七五折优惠；乙旅行社表示可先免去一位带队老师的费用，其余的入营队员八折优惠。请问应该选择哪家旅行社，才能使费用最少？
28、（6分）甲乙两地相距360km，新修的高速公路开通后，在甲乙两地行驶的汽车的平均速度提高了50%，而从甲地到乙地的时间缩短了2h。求汽车提速后的平均车速。
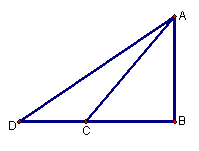29、（7分）如图，为了测量旗杆的高度，小王在离旗杆9米处的点C测得旗杆顶端A的仰角为50°；小李从C点向后退了7米到D点（B、C、D在同一直线上），量得旗杆顶端A的仰角为40°。根据这些数据，小王和小李能否求出旗杆的高度？若能，请写出求解过程；若不能，请说明理由。
 |
30、（10分）已知：如图，在梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，过O点作EF∥AD分别交AB、CD于点E、F。
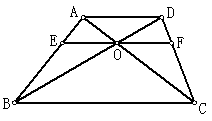（1）下面是小明对“△AOB与△DOC是否相似”的解答：
解：△AOB∽△DOC 理由如下：
∵ AD∥BC （ ）
∴ △AOD∽△COB
∴ 
（
）
又∵ ∠AOB=∠DOC （ ）
∴ △AOB∽△DOC （ ）
你认为小明的每一步解答过程是否正确？若正确，请在括号内填上理由；若不正确，请在该步骤后面的括号内打“×”。（4分）
（2）OE与OF有何关系？为什么？（4分）
（3）试求出
的值。（2分）
2004---2005学年第二学期初二年级期末考试
数 学 试 卷 参 考 答 案
一、 填空题：（每空2分，共30分）
1、＞ 2、7（a+3）（a-3） 3、（1）
；（2）
4、
；m=3；5、±14 6、2：7 7、
8、甲队 9、两条直线都垂直于同一条直线；这两条直线互相平行； 10、12cm2 ； 11、30m
12、0＜3x+4-4（x-1）＜3 或1≤3x+4-4（x-1）＜3或0＜8-x＜3
二、选择题：（每题2分，共16分，将答案直接填在下表中）
| 题号 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 | A | C | B | A | C | C | D | D |
三、解答题：（共54分）答题时须写出必要的演算过程或推理步骤
21、（4分）解：解不等式（1）得x＞-2………………（1’）
解不等式（2）得x＜5………………………（1’）
把不等式（1）、（2）的解集在同一数轴上表示出来：
所以原不等式组的解集为-2＜x＜5………………（2’）
22、（4分）解：原式＝
………………（1’）
=
………………（1’）
当x=
时：原式＝1………………（2’）
23、（4分）解分式方程：
解：方程两边同乘以
，得
………………（1’）
解这个方程，得 
………………（2’）
经检验，是原方程的增根，所以原方程无解。………………（1’）
24、（4分）（图3分、略）结论：1分。
25、（每小题1分共4分） （1）0.2； （2）50；
（3）落在第三小组（即99.5——124.5）的人数最多，是20人；（4）60%
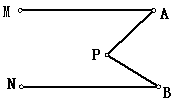26、（5分）解：（1）∠B=∠A+∠P……（1’）…
（2）∠APB=∠A+∠B（1’）
证明：（1）∵MA∥NB
|
又∵∠PQM=∠A+∠P……（1’）
∴∠B=∠A+∠P……………（1’）
或：（2）过点P作PQ∥MA，
∵ MA∥NB
∴ PQ∥MA∥NB… …（1’）
∴∠A=∠APQ……∠B=∠BPQ… （1’）
∴∠APB=∠A+∠B （1’）
27、（6分）解：设参加夏令营的有x人，总费用为y元，根据题意得：……（1’）
y甲=150x ………（1’）
y乙=160（x-1） …………（1’）
（1）若y甲= y乙 得x=16
（2）若y甲＞ y乙 得x＜16
（3）若y甲＜y乙 得x＞16 …………（1’）
答：当参加夏令营的人数等于16人时，两家旅行社的费用一样；
当参加夏令营的人数少于16人时，乙旅行社的费用较低，故选乙；
当参加夏令营的人数多于16人时，甲旅行社的费用较低，故选甲。 …（2’）
28、解：设提速前的平均车速为x km/h，根据题意得：……1`
…………2`
解得：x=60 …………1`
经检验：x=60是原方程的解，…………1`
所以，（1+50%）x=90（km/h）
答：汽车提速后的平均车速为90km/h。 ………………1`
29、（7分）解：能求出旗杆的高度。………………（1’）
根据题意可知，在△ABC中，∠ACB=50°，∠B=90°则∠BAC=40°…（1’）
在△ABC与△DBA中
∠BAC＝40°=∠D
∠B＝∠B
∴△ABC∽△DBA………………（2’）
∴
…………………（1’）
又∵BC=9 DB=7+9=16∴AB2=9×16
∴AB=12（m） ……（1’）
即旗杆的高度为12米。…………（1’）
30、（4分每空1分）
（1）（已知）；（相似三角形的对应边成比例）；（对顶角相等）；（×）
（2）OE = OF……………………（1’） 理由如下：
∵ AD∥BC
∴
∴ 
……………（1’）
又∵ EF∥AD
∴ 
……………（1’）
∴ 
∴ OF = OE……………（1’）
（3）∵ EF∥AD∥BC
∴ 
……………（1’）
∴ 
……………（1’）