2004年上虞市初二数学竞赛试卷
| 题 次 | 一 | 二 | 三 | 总 分 | |||
| 13 | 14 | 15 | 16 | ||||
| 得 分 | |||||||
| 阅卷人 | |||||||
一、选择题：（本题有6小题，每小题5分，共30分）
1、如果
，
，那么
的值为（
）
A．-2 B．-1 C．0 D．2
2、若方程2
没有实数根，则
的最小整数值为（ ）
A． -1 B．2 C．3 D．4
3、已知
，那么代数式
的值为（ ）
A． 2002 B．2003 C．2004 D．2005
4、为了调查学生的身体状况，对某校毕业生进行了体检，在前50名学生中有49名是合格的，以后每8名中有7名是合格的，且该校毕业生体检合格率在90%以上，则该校毕业生的人数最多有（ ）
A． 180 B．200 C．210 D．225
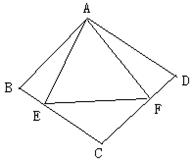
5、如图，正△AEF的边长与菱形ABCD的边长相等，点E、F分别在BC、CD上，则∠B的度数是（ ）
A． 70
B．75 C．80 D．95
6、如果
是整数，且
是
的一个因式，那么
的值为（ ）
A．-2 B．-1 C．0 D．2
二、填空题：（本题有6小题，每小题5分，共30分）
7、若关于
的方程
的解为正数，则
的取值范围是
．
8、设
，
，则
= ．
9、△ABC的周长为8，并且三边长均为自然数，则△ABC的面积为 ．
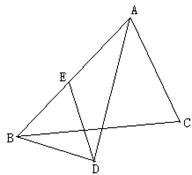10、如图，在△ABC中，AD平分∠BAC，AD⊥BD，DE∥AC交AB于E，如果AB=5，则DE的长为
．
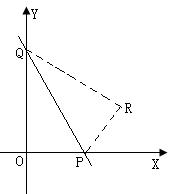
11、如图，直线
与轴、
轴分别交于P、Q两点，把△POQ沿PQ翻折，点O落在R处，则点R的坐标为
．
12、若方程组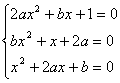
有实数解，则
=
．
三、解答题：（本题有4小题，每小题15分，共60分）
13、某商店销售某种食品，每天从食品厂批发进货，当天销售．已知进价为4.2元/千克，售价为6元/千克，当天售不完的食品可按1.2元/千克退还给食品厂．根据以往的统计，该店平均一个月（按30天计）有10天可售出食品10千克，有20天只能售出6千克，食品厂要求商店每天批进的数量相同，则该商店每天从食品厂批进这种食品多少千克，才能使每月获利最多？最多利润是多少？
14、{
，
，
，
}表示一个由
个不同的数组成的集合，仅数的排列顺序不同的集合被认为是同一集合，例如{1，2，3}与{2，3，1}是同一集合，若{
}与{
}是同一集合．试证明的的乘积为1．
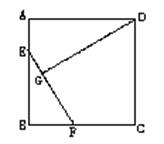15、如图，正方形ABCD中，E、F是AB、BC边上两点，已知AE=
，FC=
，连结EF且EF=3，过D作DG⊥EF于G．
（1）求正方形ABCD的边长；
（2）求四边形AEGD的面积．
16、某计算器可以接受整数对转换，并且通过按一个键遵照如下的规则来改变数对，当原来的整数对（）中的两个数之和
除以4分别余0，1，2，3时，输出的结果依次是（
），（
），（
），（
）．
（1）如果原来的整数对为（1，12），那么通过6次变换得到的整数对为（
），求的值；
（2）如果原整数对按6次键后得到的整数对为（1，17），求原整数对的值．
2004年上虞市初二数学竞赛试卷参考解答及评分意见
一、选择题：（本题有6小题，每小题5分，共30分）
1、A 2、B 3、B 4、C 5、C 6、A
二、填空题：（本题有6小题，每小题5分，共30分）
7、＜2且≠
8、
9、
10、
11、（
，
） 12、
三、解答题：（本题有4小题，每小题15分，共60分）
13、设商店每天从食品厂批进这种食品千克（60≤≤100），利润为元，则
（10分）
显然，函数随着的增大而减小．即当=60时，最多利润为=3240元．（5分）
14、由题意知：
，（5分） 
．
如果
，知
或
或z=0，当时{}＝｛0，
，0｝与题意不符（不同的数组成的集合）；同样或z=0时均不合题意，即
0．（5分）
故只能是
即的的乘积为1．（5分）
15、（1）设正方形ABCD的边长为，则BE=-，BF=-，（3分）利用勾股定理可得
（不合题意，舍去），即边长为
．（4分）延长FC到H，使CH=AE，（2分）连结DH，DF，DE，证明
DEF≌DHF和DEG≌DEA（3分）后得四边形AEGD的面积
=2
． （3分）
16、（1）从（1，12）
（1，13）（0，13）（0，14）（-1，14）
（-1，15）（-2，15），即
，所以
．（8分）
（2）逆推理，（1，17）
（1，16）（2， 16）（2，15）（3，15）
（3，14）（2，14）或（4，14），
即原整数对的值是（2，14）或（4，14）．（7分）