初二数学第四周测试题[下学期]

交大东方中学2005—2006学年度第二学期

 初二年级第四周数学测试试题

时间：70分钟　满分：100分　　总分　　　　

一、细心填一填：

1、如果不等式组的解集是，则n的取值范围是　　　　　

2、若不等式的正整数解恰好是1，2，3，则m的取值范围是　　　　 

3、多项式x²－y², x²－2xy＋y²的公因式是　　　　　 

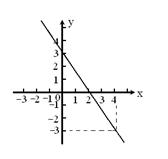
4、一次函数的图象如图所示，当－3<<3时，

的取值范围是　　　　　　　　　　 

5、若a²－2ab+b²+2(a－b)+1=0，则a－b=　　　　 

6、若不等式组的解集为－1<x<1，那么（a+1）（b－1）的值等于______.

二、解答题

1、已知代数式的值不小于的值，求x的取值范围.

2、已知，且a>2>b，请探求x的取值范围　 

3、已知关于x、y的方程组的解是正数，

（1）求的取值范围.　（2）化简

4、ａ、ｂ、ｃ为⊿ABC三边，利用因式分解说明b²－a²+2ac－c²的符号

三、把下列各式分解因式：

1、m²（x－y）＋n²（y－x）  　　　　　  2、x²(y－z)＋81(z－y)

3、　　　　　　　　　　 4、

5、

四、应用题

下表所示为装运甲、乙、丙三种蔬菜的重量及利润。某汽车运输公司计划装运甲、乙、丙三种蔬菜到外地销售（每辆汽车按规定满载，并且每辆汽车只装一种蔬菜）

	甲	乙	丙
每辆汽车能装的吨数	2	1	1.5
每吨蔬菜可获利润（百元）	5	7	4

(1)若用8辆汽车装运乙、丙两种蔬菜11吨到A地销售，问装运乙、丙两种蔬菜的汽车各多少辆？(2)公司计划用20辆汽车装运甲、乙、丙三种蔬菜36吨到B地销售（每种蔬菜不少于一车），如何安排装运，可使公司获得最大利润？最大利润是多少？

五、证明题：

1、ABCD中，E、F分别在CD、AD上，AE=CF，AE、CF交于G，连结BG，

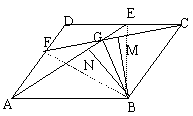求证：BG平分∠AGC。

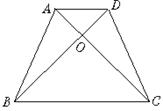
2、如图，梯形ABCD中，AD∥BC，AB=CD，对角线AC、BD相交于O，

且AC⊥BD，若AD+BC=4cm，求：（1）对角线AC的长；

（2）梯形ABCD的面积．

六、探索题

1、（本题6分）把一个多项式写成两数的和（差）的平方的形式叫做配方法，阅读下面用配方法分解因式的过程：

(1)　a²+10a+9　　　　　　　　　　　　　  (2)　x²－5x－6

=a²+2×5×a+5²－5²+9　　　　　　　　  =x²－2××x+( )²－( )²－6

=(a+5)²－4² =(x－)²－( )²

=(a+5+4)(a+5－4)　　　　　　　　　　  =(x－+)(x－+)

=(a+9)(a+1)　　　　　　　　　　　　　 =(x+1)(x－6)

请你仿照上面的方法，将下列多项式分解因式：

(1) x²－6x+8　　　　　　　　　　　　　　 (2) a²―3a―28

2、阅读下列因式分解的过程，再回答所提出的问题：

1+x+x(x+1)+x(x+1)=(1+x)[1+x+x(x+1)]=(1+x)(1+x)=(1+x)

(1)上述分解因式的方法是________，共应用了_______次.

(2)若分解1+x+x(x+1)+x(x+1)+…+ x(x+1)，则需应用上述方法______次，

结果是______　　 __

(3)分解因式：1+x+x(x+1)+x(x+1)+…+ x(x+1)(n为正整数).