东方中学第二学期初二年级
第一周检测题
班级_______ 姓名________ 分数
一、 填空题
1、如果
+x―2y―5=0，那么x－y=
；
2．已知
，则多项式
的值，
等于______________
3、若（xm÷x2n）3÷xm－n与－4x2是同类项，且2m+5n=7，
则4m2－25n2=
4、函数
与
的图像交于
轴，
则m=_______ ；
5、△ABC中，∠C=90°，∠B=30°，AD为∠BAC的平分线，
若D到AB的距离为3cm，则AD=
；
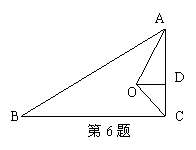
6、如图，△ABC中，∠ACB=90°，
AO、CO分别平分∠A和∠C，
OD⊥AC于D若AB=10，BC=8，
则OD= .
二、 解答题
1、
2、如图，两个直角三角形重叠在一起，将其中一个直角三角形沿着由点B到点C的方向，平移到△DEF的位置.如图所示，若AB=8，DH=3，
平移的距离BE=5.试求阴影部分的面积.
 |
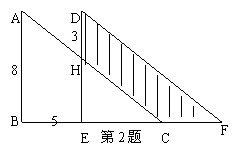3、某工程由甲、乙两队合作6天完成，厂家需付甲、乙两队共8700元；乙、丙两队合作10天完成，厂家需付乙、丙两队共9500元；甲、丙两队合作5天完成全部工程的2/3，厂家需付甲、丙两队共5500元.
（1） 求甲、乙、丙各队单独完成完成全部工程各需多少天？
（2） 若工期要求不超过15天完成全部工程，问可由哪队单独完成此项工程花钱最少？请说明理由.
4、某童装厂现有甲种布料38米，乙种布料26米，现计划用这两种布料生产L、M两种型号的童装共50套，已知做一套L型号的童装需用甲种布料0.5米，乙种布料1米，可获利45元；做一套M型号的童装需用甲种布料0.9米，乙种布料0.2米，可获利润30元。设生产L型号的童装套数为x，用这批布料生产这两种型号的童装所获利润为y（元）。
(1)写出y（元）关于x（套）的函数解析式；并求出自变量x的取值范围；
(2)该厂在生产这批童装中，当L型号的童装为多少套时，能使该厂所获的利润最大？最大利润为多少？
5、如图，在△ABC中，∠C=90°，AC=BC，自AB上任一点P作PE⊥BC于E，PF⊥AC于F，M为AB的中点.
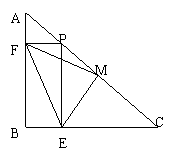求证：. △DEF为等腰三角形.
三、 探索题：已知正方形ABCD中。
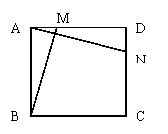（1）如图，若AN⊥BM，试说明AN=BM。
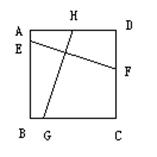（2）如图，若EF⊥GH，试说明EF=GH
(3)如上图，若EF=GH，试说明EF⊥GH