第六章 特殊平行四边形与梯形测试题
一、选择题（每小题3分，共30分）
1．下列说法中，不正确的是（ ）．
（A）有三个角是直角的四边形是矩形;（B）对角线相等的四边形是矩形
（C）对角线互相垂直的矩形是正方形;（D）对角线互相垂直的平行四边形是菱形
2．已知一个四边形的对角线互相垂直，那么顺次连接这个四边形的四边中点所得的四边形是（ ）．
（A）矩形 （B）菱形 （C）等腰梯形 （D）正方形
3．用两个全等的直角三角形拼下列图形：①矩形；②菱形；③正方形；④平行四边形；⑤等腰三角形；⑥等腰梯形．其中一定能拼成的图形是（ ）．
（A）①②③ （B）①④⑤ （C）①②⑤ （D）②⑤⑥
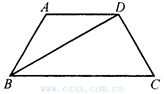
4．如图1，在梯形ABCD中，AD∥BC，AB=DC，∠C=60°，BD平分∠ABC．如果这个梯形的周长为30，则AB的长为（ ）．
（A）4 （B）5 （C）6 （D）7
(1) (2) (3)
5．如图2，矩形ABCD沿AE折叠，使点D落在BC边上的F点处，如果∠BAF=60°，那么∠DAE等于（ ）．
（A）15° （B）30° （C）45° （D）60°
6．如图3，在菱形ABCD中，∠ADC=120°，则BD：AC等于（ ）．
（A）
：2 （B）：3 （C）1：2 （D）：1
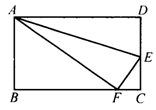
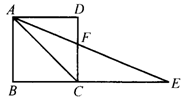
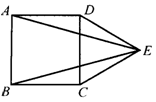
7．如图4，四边形ABCD是正方形，延长BC至点E，使CE=CA，连结AE交CD于点F，则∠AFC的度数是（ ）．
（A）150° （B）125° （C）135° （D）112．5°
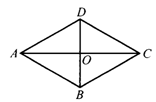
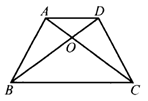
8．如图5，在等腰梯形ABCD中，AD∥BC，AC，BD相交于点O．有下列四个结论：①AC=BD；②梯形ABCD是轴对称图形；③∠ADB=∠DAC；④△AOD≌△ABO．其中正确的是（ ）．
（A）①③④ （B）①②④ （C）①②③ （D）②③④
(4) (5)
9．一张矩形纸片按如图甲或乙所示对折，然后沿着图丙中的虚线剪下，得到①，②两部分，将①展开后得到的平面图形是（ ）．
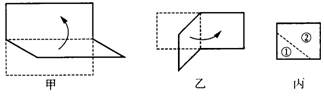
（A）三角形 （B）矩形 （C）菱形 （D）梯形
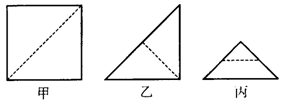
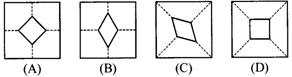
10．小许拿了一张正方形的纸片如图甲，沿虚线对折一次得图乙．再对折一次得图丙．然后用剪刀沿图丙中的虚线（虚线与底边平行）剪去一个角．打开后的形状是（ ）．
二、填空题（每小题3分，共30分）
11．既是轴对称图形，又是中心对称图形的四边形是_________．
12．把“直角三角形、等腰三角形、等腰直角三角形”填入下列相应的空格上：
（1）正方形可以由两个能够完全重合的_________拼合而成；
（2）菱形可以由两个能够完全重合的_________拼合而成；
（3）矩形可以由两个能够完全重合的________拼合而成．
13．在
ABCD中，若添加一个条件________，则四边形ABCD是矩形；若添加一个条件_______，则四边形ABCD是菱形．
14．已知正方形的面积为4，则正方形的边长为________，对角线长为________．
15．已知矩形的对角线长为4cm，一条边长为2cm，则面积为________．
16．菱形的两条对角线分别是6cm，8cm，则菱形的边长为_____，面积为______．
17．如图6，在四边形ABCD是正方形，△CDE是等边三角形，则∠AED=______，∠AEB=______．
(6) (7) (8)
18．如图7，在等腰梯形ABCD中，AD∥BC，AD=6cm，BC=8cm，∠B=60°，则AB=_______cm．
19．现有一张长53cm，宽28cm的矩形纸片，要从中剪出长15cm，宽12cm的矩形小纸片，则最多能剪出______张．
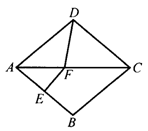
20．如图8，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，E为垂足，连结DF，则∠CDF的度数=________．
三、解答题（40分）
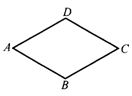
21．（6分）如图，在菱形ABCD中，∠A与∠B的度数比为1：2，周长是48cm．求：
（1）两条对角线的长度；（2）菱形的面积．
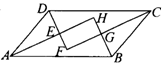
22．（8分）已知：如图，ABCD各角的平分线分别相交于点E，F，G，H，求证：四边形EFGH是矩形．
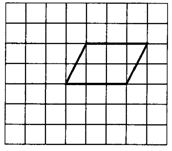
23．（8分）如图，适当地改变方格图中的平行四边形的部分位置，并保持面积不变，先使其成为矩形，再将矩形向下平移3个格后，继续改变其中某些部分的位置并保持面积不变，使其成为菱形．说明在变化过程中所运用的图形变换．
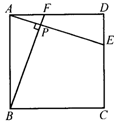
24．（8分）已知：如图，在正方形ABCD中，AE⊥BF，垂足为P，AE与CD交于点E，BF与AD交于点F，求证：AE=BF．
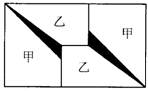
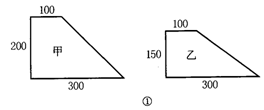
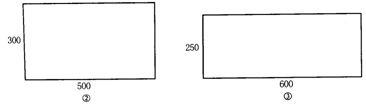
25．（10分）如图，要剪切如图①（尺寸单位：mm）所示的甲、乙两种直角梯形零件，且使两种零件的数量相等．有两种面积相等的矩形铝板，第一种长500mm，宽300mm（如图②）；第二种长600mm，宽250mm（如图③）可供选用．
（1）填空：为了充分利用材料，应选用第______种铝板，这时一块铝板最多能剪甲、乙两种零件共_______个，剪下这些零件后，剩余的边角料的面积是______mm2．
（2）画图：从图②或图③中选出待用的铝板示意图，在图上画出剪切线，并把边角余料用阴影表示出来．
答案:
1．B 2．A 3．B 4．C 5．A 6．B 7．D 8．C 9．C 10．D
11．答案不唯一
12．（1）等腰直角三角形 （2）等腰三角形 （3）直角三角形
13．AC=BD；AB=BC
14．2；2
15．4cm2
16．5cm；24cm2
17．15°；30°
18．2
19．4
20．60°
21．（1）BD=12cm，AC=12cm （2）S菱形ABCD=72cm2
22．略
23．图略
24．提示：只要证明△ABF≌△DAE
25．提示：（1）选用第一种铝板，最多能剪甲、乙两种零件各2个，共4个，
如图所示．S阴=300×500-2×
×200-2××150=10 000（mm）2
（2）剪切线如图所示:
