八年级1-4章中的中考试题
1、
解方程:![]() (广东常德)
(广东常德)
2、
解方程:![]() (广东佛山)
(广东佛山)
3、
化简:![]() (广东佛山)
(广东佛山)
4、下列分式的运算中,其中结果正确的是:(广东茂名)
A 、![]() , B、
, B、![]() , C、
, C、![]() ,D、
,D、![]()
5、
方程:![]()
6、
先化简,再求值:(![]() )÷
)÷![]() ,其中x=2005。
,其中x=2005。
7、已知两个分式:A=![]() ,B=
,B=![]() ,其中x≠±2.
,其中x≠±2.
下面有三个结论:①A=B; ②A、B互为倒数; ③A、B互为相反数.
请问哪个正确?为什么?
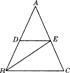 8、 如图,在△ABC中,AB=AC,BE平分∠ABC,DE∥BC.
8、 如图,在△ABC中,AB=AC,BE平分∠ABC,DE∥BC.
求证:DE=EC.
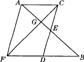 9、如图,AB与CD相交于E,AE=EB,CE=ED,D为线段FB的中点,CF与AB交于点G,若CF=15cm,求GF之长.
9、如图,AB与CD相交于E,AE=EB,CE=ED,D为线段FB的中点,CF与AB交于点G,若CF=15cm,求GF之长.
10、化简: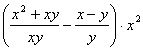
 11、有一道题“先化简,再求值:
11、有一道题“先化简,再求值:![]() ,其中
,其中![]() 。”小玲做题时把“
。”小玲做题时把“![]() ”错抄成了“
”错抄成了“![]() ”,但她的计算结果也是正确的,请你解释这是怎么回事?(河南)
”,但她的计算结果也是正确的,请你解释这是怎么回事?(河南)
12、已知x=3是方程![]() 的一个根,求k的值和方程其余的根(甘肃兰州)
的一个根,求k的值和方程其余的根(甘肃兰州)
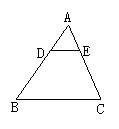
13、.如图:D是△ABC的AB边上的一点,过点D作DE∥BC交AC于E, 若AD:DB=1:2,则BC:DE等于( )
A.1:3 B.2:3 C.3:1 D.2:1(湖北黄石)
14、.解方程![]() ,如果设
,如果设![]() ,那么原方程组可化为( )
,那么原方程组可化为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() (湖北黄石)
(湖北黄石)
15、先化简再求值.![]() ,其中
,其中![]() .(湖北黄石)
.(湖北黄石)
16、平面直角坐标系中的点P![]() 关于
关于![]() 轴的对称点在第四象限,则
轴的对称点在第四象限,则![]() 的取值范围在数轴上可表示为( )
的取值范围在数轴上可表示为( )
 |
 17、分解因式:
17、分解因式:![]() =
.
=
.
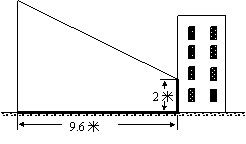
18、赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为 米.
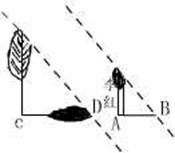
![]() 18、如图,已知线段AB,点C在AB上,且有
18、如图,已知线段AB,点C在AB上,且有![]() ,则
,则![]() 的数值为
;若AB的长度与中央电视台演播厅舞台的宽度一样长,那么节目主持人应站在
位置最好。
的数值为
;若AB的长度与中央电视台演播厅舞台的宽度一样长,那么节目主持人应站在
位置最好。
19、在一个宁静的夜晚,月光明媚,张芳和身高为1.65m的李红两位同学在人民广场上玩。张芳测得李红的影长为1m,并立即测得小树影长为1.5m,请你估算小树的高约为多少?
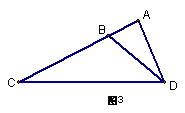 20、如图3,已知△ACP∽△ABC,AC = 4,AP = 2,则AB的长为
.
20、如图3,已知△ACP∽△ABC,AC = 4,AP = 2,则AB的长为
.
21、先化简,再求值:![]() ,其中
,其中![]() ,
,![]()
22、若 ,则的值是( )
A、 B、 C、 D、
23、不等式组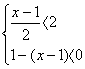 的解集是( )
的解集是( )
A.2<x<5 B.0<x<5 C.2<x<3 D.x<2
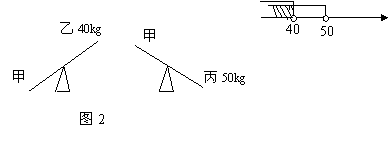
24、图2是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),
则甲的体重的取值范围在数轴上表示正确的是( )
 | |||
 | |||
A B
 | |||
 | |||
25、为了加强学生的交通安全意识,某中学和交警大队联合举行了“我当一日小交警”活动,星期天选派部分学生到交通路口值勤,协助交通警察维护交通秩序.若每一个路口安排4人,那么还剩下78人;若每个路口安排8人,那么最后一个路口不足8人,但不少于4人.求这个中学共选派值勤学生多少人?共有多少个交通路口安排值勤?
26、某工厂生产的某种产品按质量分为![]() 个档次,生产第一档次(即最低档次)的产品一天生产
个档次,生产第一档次(即最低档次)的产品一天生产![]() 件,每件利润
件,每件利润![]() 元,每提高一个档次,利润每件增加
元,每提高一个档次,利润每件增加![]() 元.
元.
(1)每件利润为![]() 元时,此产品质量在第几档次?
元时,此产品质量在第几档次?
(2)由于生产工序不同,此产品每提高一个档次,一天产量减少![]() 件.若生产第
件.若生产第![]() 档的产品一天的总利润为
档的产品一天的总利润为![]() 元(其中
元(其中![]() 为正整数,且
为正整数,且![]() ≤
≤![]() ≤
≤![]() ),求出
),求出![]() 关于
关于![]() 的函数关系式;若生产某档次产品一天的总利润为
的函数关系式;若生产某档次产品一天的总利润为![]() 元,该工厂生产的是第几档次的产品?
元,该工厂生产的是第几档次的产品?
 27、已知x=
27、已知x=![]() ,求
,求![]() 的值.
的值.
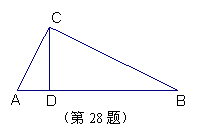
28、如图, 在Rt△ABC中, ∠ACB=90°,CD⊥AB于D,
若AD=1,BD=4,则CD=
(A)2 (B)4
(C)![]() (D)3
(D)3
29、班共有50名学生,老师安排每人制作一件![]() 型或
型或![]() 型的陶艺品,学校现有甲种制作材料36㎏,乙种制作材料29㎏,制作
型的陶艺品,学校现有甲种制作材料36㎏,乙种制作材料29㎏,制作![]() 、
、![]() 两种型号的陶艺品用料情况如下表:
两种型号的陶艺品用料情况如下表:
| 需甲种材料 | 需乙种材料 | |
| 1件 | 0.9 | 0.3 |
| 1件 | 0.4 | 1 |
(1)设制作![]() 型陶艺品
型陶艺品![]() 件,求
件,求![]() 的取值范围;
的取值范围;
(2)请你根据学校现有材料,分别写出七(2)班制作![]() 型和
型和![]() 型陶艺品的件数.
型陶艺品的件数.
30、解不等式组,并把解集在数轴上表示出来
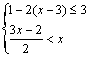
31.先化简,再请你用喜爱的数代入求值
![]()
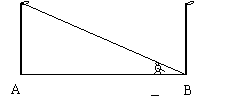 32、如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A 25米,离路灯B 5米,如果小亮的身高为1.6米,那么路灯高度为
32、如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A 25米,离路灯B 5米,如果小亮的身高为1.6米,那么路灯高度为
A.6.4米
B. 8米
C.9.6米
D. 11.2米
33、苏州地处太湖之滨,有丰富的水产养殖资源,水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖,他了解到如下信息:
①每亩水面的年租金为500元,水面需按整数亩出租;
②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗;
③每公斤蟹苗的价格为75元,其饲养费用为525元,当年可获1400元收益;
④每公斤虾苗的价格为15元,其饲养费用为85元,当年可获160元收益;
(1)若租用水面n亩,则年租金共需 元;
(2)水产养殖的成本包括水面年租金、苗种费用和饲养费用,求每亩水面蟹虾混合养殖的年利润(利润:收益—成本);
(3)李大爷现有资金25000元,他准备再向银行贷不超过25000元的款。用于蟹虾混合养殖。已知银行贷款的年利率为8%,试问李大爷应该租多少亩水面,并向银行贷款多少元.可使年利润超过35000元?
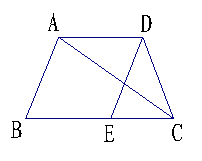 34、若关于
34、若关于![]() 的方程
的方程![]() 有增根,则
有增根,则![]() 的值是
的值是
A.3 B.2
C.1 D.-1
35、如图,梯形ABCD中,AD∥BC,AB=DC,∠ADC=120°,对角线CA平分∠DCB,E为BC的中点,试求△DCE与四边形ABED面积的比。
36、已知实数a满足a2+2a-8=0,求![]() 的值.
的值.
37、已知某项工程由甲、乙两队合做12天可以完成,共需工程费用13800元,乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的2倍少10天,且甲队每天的工程费用比乙队多150元.
(1) 甲、乙两队单独完成这项工程分别需要多少天?
(2) 若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应该选择哪个工程队?请说明理由.
38、为了解决农民工子女入学难的问题,我市建立了一套进城农民工子女就学的保障机制,其中一项就是免交“借读费”。据统计,2004年秋季有5000名农民工子女进入主城区中小学学习,预测2005年秋季进入主城区中小学学习的农民工子女将比2004年有所增加,其中小学增加20%,中学增加30%,这样,2005年秋季将新增1160名农民工子女在主城区中小学学习。
(1)如果按小学每生每年收“借读费”500元,中学每生每年收“借读费”1000元计算,求2005年新增的1160名中小学生共免收多少“借读费”?
(2)如果小学每40名学生配备2名教师,中学每40名学生配备3名教师,若按2005年秋季入学后,农民工子女在主城区中小学就读的学生人数计算,一共需要配备多少名中小学教师?
39、宏志高中高一年级近几年来招生人数逐年增加,去年达到550名,其中面向全省招收的”宏志班”学生,也有一般普通班学生.由于场地,师资等限制,今年招生最多比去年增加100人,其中普通班学生可多招20%,”宏志班”学生可多招10%,问今年最少可招收”宏志班”学生多少名?
40、某高速公路收费站,有m(m>0)辆汽车排队等候收费通过。假设通过收费站的车流量(每分钟通过的汽车数量)保持不变,每个收费窗口的收费检票的速度也是不变的。若开放一个收费窗口,则需20分钟才可能将原来排队等候的汽车以及后来接上来的汽车全部收费通过;若同时开放两个收费窗口,则只需8分钟也可将原来排队等候的汽车以及后来接上来的汽车全部收费通过。若要求在3分钟内将排队等候收费的汽车全部通过,并使后来到站的汽车也随到随时收费通过,请问至少要同时开放几个收费窗口?
41、某市为处理污水需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时每天比原计划多铺设10米,结果提前20天完成任务。设原计划每天铺设管道x米,则可得方程( )
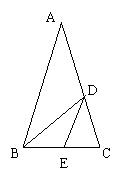
![]() (A)
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
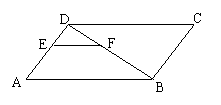
42、顶角为36°的等腰三角形称为黄金三角形。如
图,△ABC、△BDC、△DEC都是黄金三角形
已知AB=1,则DE=___________________
 43、如图,在 ABCD中,EF∥AB,DE∶EA = 2∶3,EF = 4,则CD的长为( )
43、如图,在 ABCD中,EF∥AB,DE∶EA = 2∶3,EF = 4,则CD的长为( )
A. B.8 C.10 D.16
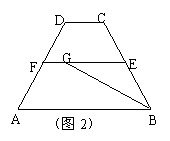 |
44、如图2,已知EF是梯形ABCD的中位线,若AB=8,BC=6,
CD=2,∠B的平分线交EF于G,则FG的长是( )
A.1 B.1.5 C.2 D.2.5
 45、如图1,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,
45、如图1,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,
B点恰好落在AB的中点E处,则∠A等于 ( )
A.25° B.30° C.45° D.60°
46.不等式组![]() 的解集表示在数轴上正确的 ( )
的解集表示在数轴上正确的 ( )
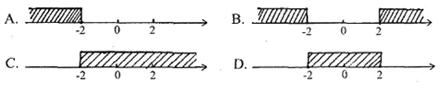
47、为了解中学生的体能情况,某校随机抽取了部分学生进行一分钟跳绳次数测试.某同学将所得的数据进行整理,列出下表(未完成):
| 分组(跳绳次数x) | 频数(学生人数) | 频 率 |
| 60≤x<80 | 2 | |
| 80≤x<100 | 0.1 | |
| 100≤x<120 | 17 | 0.34 |
| 120≤x<140 | 0.3 | |
| 140≤x<160 | 8 | 0.16 |
| 160≤x<180 | 3 | n |
| 合计 | m |
(1)求出上表中m,n的值;
 (2)一分钟跳绳次数小于100的学生人数占被测试学生总数的百分之几?
(2)一分钟跳绳次数小于100的学生人数占被测试学生总数的百分之几?
(3)这次测试中,学生跳绳次数的中位数落在哪个范围内?并说明理由.
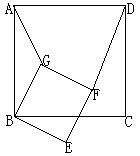
48、如图,四边形ABCD和BEFG均为正方形,则![]() =________。(结果不取近似值)
=________。(结果不取近似值)