重庆一中初2007级月考数学试题
时间120分钟 满分150分
一．选择题（本题共10小题，每小题4分，共40分。每小题只有一个答案是正确的，请将正确答案填入括号里）
1．下列说法正确的是 （ ）
A．4是16的算术平方根 B．10的平方根为±5
C．绝对值是2的数一定为2 D．8的立方根为±2
2．下列美丽的图案，既是轴对称图形又是中心对称图形的个数是 （ ）
 |
A．1个 B．2个 C．3个 D．4个
3．如图，□ABCD的周长为16cm，AC．BD相交于点O，
OE⊥AC交AD于E，则△DCE的周长为（ ）
A．4cm B．6cm
C．8cm D．10cm
4．下列四对数中，是方程组
的解的是（ ）
A．
B．
C．
D．
5．利用边长相等的正三角形和正六边形的地砖镶嵌地面时，在每个顶点周围有a块正三角形和b块正六边形的地砖（ab≠0），则a+b的值为（ ）
A．3或4 B．4或5 C．5或6 D．4
6．已知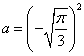
，
，
，则a，b，c的大小关系是（ ）
A．a>b>c B．b>a>c C．a>c>b D．b>c>a
7．给出下面四个命题:(1)一组对边平行的四边形是梯形;(2)一条对角线平分一个内角的平行四边形是菱形;(3)两条对角线互相垂直的矩形是正方形;(4)一组对边平行,另一组对边相等的四边形是平行四边形,其中正确的个数有( )
A．1个 B．2个 C．3个 D．4个
8．等腰梯形
中，
，高
，则该梯形的下底角为
（ ）
A．
B．
C．
D．
9．已知
的解是方程
的一个解，则
=( )
A．1 B．2 C．3 D．4
10．矩形ABCD中，R、P分别是DC、BC上的点，E、F分别是AP、RP的中点，当P在BC上从B向C移动而R不动时，下列结论成立的是（ ）
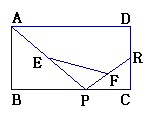A．线段EF的长不断增大
B．线段EF的长不断减小
C．线段EF的长不变
D．线段EF的长不能确定
二．填空题（本题共10小题，每小题4分，共40分，请将正确答案填在相应的横线上）
11．下列各数：
、
、
、
、0.…中是无理数的有
个.
12．如果一个多边形的内角和为1440o，那么这个多边形的边数为 .
13．如图，数轴上表示1、
的对应点分别为A、B，点B关于点A的对应点为C，设
点C所表示的数为,那么
__________.
 |
14．若方程
是二元一次方程，则
= .
15．已知菱形的一个内角为60o，且一条对角线的长度为3cm，则菱形的面积为
.
16．如图，正方形中，
在对角线
上，
那么
_______________
17．已知方程组
与
的解相同，则
的值为
.
18．如图，矩形ABCD两邻边分别为3、4, 点P是矩形一边
上任意一点，则点P到两条对角线AC、BD的距离之和
PE+PF为 .
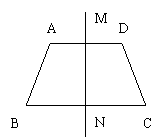19．如图，梯形ABCD中，AD∥BC，AB=CD=AD=1，
∠B=60o， 直线MN为梯形ABCD的对称轴，P为MN
上一点，那么PC+PD的最小值为 .
20．甲、乙、丙三人共解出100道数学题，每人都解出了其中的60道题，将其中1人解出的题叫做难题，3人解出的题叫做容易题，则难题比容易题多 道.
三．解答题（本大题共8小题，每小题10分，共80分）
21．计算下列各题：
（1）
（2）
22．解下列方程组：
（1）
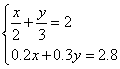（2）
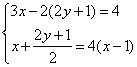
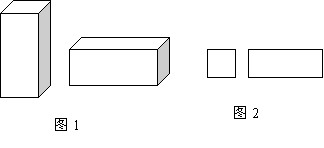
23．某纸品加工厂为了制作甲、乙两种无盖的长方体小盒（如图1所示），利用边角废料裁出正方形和长方形两种硬纸片（如图2所示），长方形的宽和正方形的边长相等. 现将150张正方形硬纸片和300张长方形硬纸片全部用于制作两种小盒，可以各做多少个？
 |
|
24．已知方程组
，由于小明看错了方程①中的a，得到方程组的解为
，小芳看错了方程②中的b，得到方程组的解为
，请问：原方程组的解应该是多少？
25．观察下列图形的变化过程，解答以下问题：
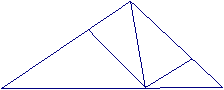
如图,在△ABC中,D为BC边上的一动点(D点不与B、C两点重合)，DE//AC交AB于E点，DF//AB交AC于F点．
（1）试探索AD满足什么条件时，四边形AEDF为菱形，并说明理由；
（2）在（1）的条件下，△ABC满足什么条件时，四边形AEDF为正方形，为什么？
26．为了解决农民工子女入学难的问题，我市建立了一套进城农民工子女就学保障机制，其中一项就是免交“借读费”.据统计2004年秋季有5000名农民工子女进入主城区中小学学习，预测2005年秋季进入主城区中小学学习的农民工子女将比2004年有所增加，其中小学增加20%，中学增加30%，这样，2005年秋季将新增1160名农民工子女在主城区中小学学习.
(1)如果按小学每生每年收“借读费”500元，中学每生每年收“借读费”1000元计算，求2005年新增的1160名中小学生共免收多少“借读费”？
(2)如果小学每40名学生配备2名教师，中学每40名学生配备3名教师，若按2005年秋季入学后，农民工子女在主城区中小学就读的学生人数计算，一共需要配备多少名中小学教师？
27．已知菱形ABCD，
=，把一个含有角的三角尺与这个菱形叠合，使三角尺的角的顶点与点A重合，三角尺的一边与AB重合. 现将三角尺绕点A按逆时针方向旋转.
（1）当三角尺的两边分别与菱形的两边BC、CD相交于点E、F时(如图①)，通过观察或测量BE、CF的长度你能得出什么结论？并证明你的结论.
（2）在（1）问的条件下，四边形AECF的面积有何变化？证明你发现的结论.
（3）当三角尺的两边分别与菱形的两边BC、CD的延长线相交于点E、F时(如图②)，你在（1）中得到的结论还成立吗？请简要说明理由.
 |
28．某商场计划拨款9万元从厂家购进50台电视机，已知该厂家生产三种不同型号的电视机，出厂价分别为：甲种每台1500元，乙种每台2100元，丙种每台2500元.
(1)若商场同时购进其中两种不同型号的电视机共50台，用去9万元，请你研究一下商场的进货方案？
(2)若商场销售一台甲种电视机可获利150元，销售一台乙种电视机可获利200元，销售一台丙种电视机可获利250元，在同时购进两种不同型号的电视机的方案中，为使销售时获利最多，你选择哪种进货方案？
(3)若商场准备用9万元同时购进三种不同型号的电视机50台，请你设计进货方案？
友情提示：祝贺你，终于将考题做完了，请你再仔细的检查一遍，看看有没有错的、漏的，可要仔细点！