2006年（下）下陈中学初二数学竞赛试卷
班级 姓名 学号
一、填空题：（每小题3分，共30分）
1、x=3-2a是不等式
(x-3)<x-
的解，那么a的取值范围是___________。
2、若a、b都为正实数，且
，则
=_________。
3、化简
__________。
4、若质数m、n满足5m+7n=129, 则m+n的值为_________。
5、在△ABC中，AB=AC，AB的垂直平分线与AC所在的直线交得的锐角为60o，则底角∠B=_________。
6、两个角
的补角互余，则这两个角的和
大小是
。
7、在正五边形ABCDE所在平面内能找到点P，使得△PCD与△BCD的面积相等，并且△ABP为等腰三角形，这样的点P共有_____ 个。
8、一只小船顺流航行在甲、乙两个码头之间需a小时，逆航这段距离需b小时，那么一木头顺水漂流这段路程需_____小时。
9、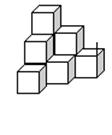
学校食堂出售两种厚度一样但大小不同的面饼,小饼直径
,售价30分;大饼直径
,售价40分.你更愿意买
饼,原因是
。
10、把正方体摆放成如图的形状，若从上至下依次为第1层，第2层，第3层，……，则第n层有 个正方体。
二、选择题：（单项选择题，每小题3分，共30分）
|
答案 |
题号 1 2 3 4 5 6 7 8 9 10
1、若
、
、
、
都是有理数，并且
，
，则与
A、互为倒数 B、互为负倒数 C、互为相反数 D、相等
2、已知x2+ax-12能分解成两个整数系数的一次因式的积，则符合条件的整数a的个数是（ ）。
A、3个 B、4个 C、6个 D、8个 A
3、等腰三角形底边长5cm，一腰上的中线把其周长分为两部分之差为3cm，则腰长为（ ）。
A、2cm B、8cm C、2cm或8cm D、以上都不对
4、已知关于
的方程
有唯一解，那么
的值的情况是（
）。
（A）
（B）
（C）
或
（D）且
5、已知
是任意实数，有4个不等式：①
；②
；③
；④
，那么不等式关系一定成立的有（
）个。
（A）1 （B）2 （C）3 （D）4
6、把自然数
的各位数字之和记为
如
7＝13，若对于某些自然数满足
则的最大值是（
）
（A）2025 （B）2023 （C）2021 （D）2019
7、设
则
的关系是（
）
（A）
（B）
（C）
（D）
8、周长为4的不等边四边形，其最长边的长度取值范围是（ ）
(A)1<x<2 (B)1<x≤2
(C)1≤x≤2 (D)1≤x<2
9、某商品有两个进价不同的计算器都卖了64元，其中一个盈利60%，另一个夸本20%，在这次买卖中，这家商店
（A）不赔不赚 （B）赚了8元
（C）赔了8元 （D）赚了32元
10、某超级市场失窃，大量的商品在夜间被罪犯用汽车运走。三个嫌疑犯被警察局传讯，警察局已经掌握了以下事实：(1)罪犯不在A、B、C三人之外；(2)C作案时总得有A作从犯；(3)B不会开车。在此案中能肯定的作案对象是（ ）
A．嫌疑犯A B．嫌疑犯B C．嫌疑犯C D．嫌疑犯A和C
三、简答题（4小题，共40分）
1、我校学生去军训。要求大宿舍住的学生数相同，开始每舍住22人，结果剩下一人未被分到住处。如果用一宿舍做小会议室，那么正好平均把全体学生分到各宿舍。已知每个宿舍最多住32人，问有多少学生参加军训？给准备了多少间宿舍？（本小题8分）
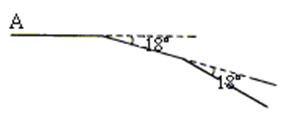
2、 如右图，某同学从A点出发前进10 米，向右转18°，再前进10米，又向右转18°，这样下去，他第一次回到出发点A时，一共走了多少米？（本小题8分）
3、（本题满分12分）某超市对顾客实行优惠购物，规定如下：
（1）若一次性购物少于200元，则不予优惠；
（2）若一次性购物满200元，但不超过500元，按标价给予9折优惠；
（3）若一次性购物超过500元，其中500元以下部分（包括500元）按标价给予9折优惠，超过500元部分按标价给予8折优惠。
李明两次去超市购物，分别付款198元和554元，现在王娟准备一次性地购买和李明分两次购买同样多的物品，她需付款多少元？
4、(本小题满分12分)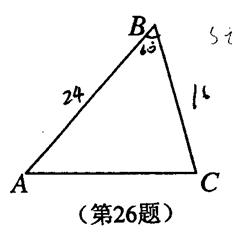
在三角形ABC中, 
.现有动点P从点A出发,沿射线AB向点B方向运动;动点Q从点C出发,沿射线CB也向点B方向运动.如果点P的速度是
/秒,点Q的速度是
/秒,它们同时出发,求:
(1)几秒钟后,ΔPBQ的面积是ΔABC的面积的一半?
(2)在第(1)问的前提下,P,Q两点之间的距离是多少？