《平行四边形》单元测试题
一、填空题(每题3分,共30分)
1.已知在
中,AB=14
,BC=16,则此平行四边形的周长为
.
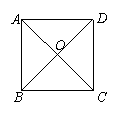
2.如图,正方形ABCD的对线AC、BD相交于点O.
那么图中共有 个等腰直角三角形.
3.矩形的两条对角线的夹角为
,
较短的边长为12,则对角线长为 .
(第2题)
4.若直角梯形被一条对角线分成两个等腰直角三角形,那么这个梯形中除两个直角外,其余两个内角的度数分别为 
和 .
5.平行四边形的周长为24,相邻两边长的比为3:1,那么这个平行四边形较短的边长为
.
6.根据图中所给的尺寸和比例,可知这个“十”字标志的周长为
.
L
(第6题)
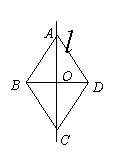
(第8题)
7.已知菱形的两条对角线长为12和6,那么这个菱形的面积为
.
8.如图,L 是四边形ABCD的对称轴,如果AD∥BC,有下列结论: (1)AB∥CD;(2)AB=CD;(3)AB
BC;(4)AO=OC.其中正确的结论是
.
(把你认为正确的结论的序号都填上)
9、菱形ABCD的周长为36，其相邻两内角的度数比为1:5，则此菱形的面积为____________。
10、已知菱形两条对角线长分别是4cm和8cm，则它的边长为__________。
二、选择题(每题3分,共30分)
11.下列说法中,错误的是 ( )
A.平行四边形的对角线互相平分 B.对角线互相平分的四边形是平行四边形
C.菱形的对角线互相垂直 D.对角线互相垂直的四边形是菱形
12.给出四个特征(1)两条对角线相等;(2)任一组对角互补;(3)任一组邻角互补;(4)是轴对称图形但不是中心对称图形,其中属于矩形和等腰梯形共同具有的特征的共有 ( )
A.1个 B.2个 C.3个 D.4个
13.如果一个四边形的两条对角线互相平分,互相垂直且相等,那么这个四边形是 ( )
A.矩形 B.菱形 C.正方形 D.菱形、矩形或正方形
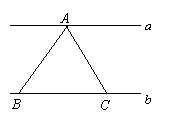
14.如图,直线
∥
,A是直线上的一个定点,线段BC在直线上移动,那么在移动过程中
的面积
|
 | |||
| |||
(第14题) (第15题) (第16题)
15.如图,矩形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果
,则
等于 A.
B.
C.
D.
( )
16.如图,在中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是
( )
A.5 B.10 C.15 D.20
17、顺次连结任意四边形四边中点所得的四边形一定是（ ）
A、平行四边形 B、矩形 C、菱形 D、正方形
 |
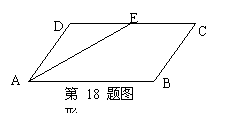
18、如图，平行四边形ABCD中，∠A的平分线AE交CD于E，AB=5，BC=3，则EC的长（ ）
A、1 B、1.5 C、2 D、3
19、等腰梯形的两底之差等于腰长，则腰与下底的夹角为（ ）
A、120° B、60° C、45° D、135°
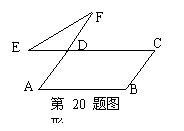
20、在平行四边形ABCD中,∠B=110O,延长AD至F,延长CD至E,连接EF,则∠E+∠F=（ ）
A、110O B、30O C、50O D、70O
三、解答题(第19题8分,第20~23题每题10分,共48分)
21、（8分）已知：如图，梯形ABCD中，AD∥BC，∠B=60°，∠C=30°，AD=2，BC=8。
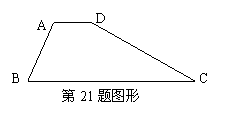求：梯形两腰AB、CD的长。
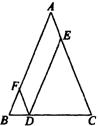
22.如图, 中,DB=CD,
,AE⊥BD于E.
|
的度数.
|
.
(1)试说明DF=BG; (2)试求
的度数.
(第23题)
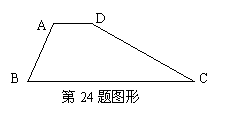
24. 已知：如图，梯形ABCD中，AD∥BC，∠B=60°，∠C=30°，AD=5，BC=11。
求：梯形两腰AB、CD的长。
25.如图,直线MN经过线段AC的端点A,点B、Ｄ分别在
和
的角平分线AE、AF上,BD交AC于点O,如果O是BD的中点,试找出当点O在AC的什么位置时,四边形ABCD是矩形,并说明理由.
|
