泽国镇八年级数学第二次调研试卷
卷首语：亲爱的同学，祝贺你完成了前面知识的学习，现在是展现你学习成果之时，尽情的发挥吧，祝你成功！
一、精心选一选（每小题3分，共30分）
1．人体中成熟红细胞的平均直径为 0. m ,用科学记数法表示 （ ）
A．7.7×10 -5 m B. 77×10 - 6 m C. 77×10_5 m D. 7.7×10-6 m
2下列各组数中能作为直角三角形三边长的是 （ ）
A．3，4，5 B．5，7，12 C．7，15，17 D．8，12，15
3.矩形具有而菱形不一定具有的性质是 （ ）
A、对角线互相平分 B、对边相等
C、对角线相等 D、对角线互相垂直
4.如图，矩形ABCD沿AE折叠，使D点落在BC边上的F点处，如果∠BAF=60
则∠DAE等于（ ）
A、150 B、300 C、450 D、60
5、在平行四边形ABCD中，∠B=110º，延长AD至F，延长CD至E，连接EF则∠E+∠F= （ ）
A、110º B、30º C、50º D、70º
6. 如图，在一个由4×4个小正方形组成的正方形网格中，阴影部分面积与正方形ABCD的面积比是 （ ）
A、3：4 B、5：8 C、9：16 D、1：2
 |
7. 如图，以直角三角形三边为边长作正方形，其中两个以直角边为边长的
正方形面积分别为225和400，则正方形
的面
积是 （ ）
A. 175 B.575 C. 625 D.700
8．将一张菱形的纸片折一次，使得折痕平分这个菱形的面积，则这样的折纸方法共有（ ）
A、1种 B、2种 C、4种 D、无数种
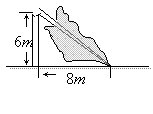
9．由于台风的影响，一棵树在离地面
处折断，树顶落在离树干底部
处，则这棵树在折断前（不包括树根）长度是
（ ）
A. B.
C.
D.
10.某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P（kPa）是气体体积V(m3)的反比例函数，其图像如图所示，当气球内的气压大于140KPa时，气球将爆炸，为了安全起见，气体体积应 （ ）
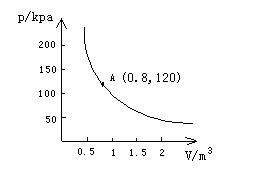A、不大于
B、不小于
C、不大于
D、不小于
二、耐心填一填（每空3分，共30分）
11、当x_______________时，分式
有意义。
12、写出一个反比例函数，使y随着x的增大而减少：_______________
13、菱形的对角线长分别为6和8，则菱形的面积为：_______________
14、写出命题“如果两个实数相等，那么它们的绝对值相等”的逆命题：
_________________________________________________
15、已知平行四边形两邻边的比是2:3,它的周长是40cm,则该平行四边形较长边的长是
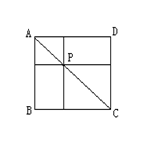
16、如图，正方形ABCD中，AB=1，点P是对角线AC上一点，分别以AP、PC为对角线作正方形，则两个小正方形的周长的和是
17、一根蜡烛在凸透镜下成一实像，物距u像距v和凸透镜的焦距f满足关系式：
，若f=6厘米，v=8厘米则物距u= 厘米。
18、若将四根木条钉成的矩形木框变形为平行四边形的形状，并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角的值等于 .
 | |||||
 | |||||
 | |||||
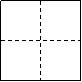19、将一张正方形纸片剪成四个大小形状一样的小正方形，然后将其中的一片又按同样的方法剪成四小片，再将其中的一小片正方形纸片剪成四片，如此循环进行下去，结果如下表：
| 所剪次数 | 1 | 2 | 3 | 4 | 5 | … |
| 正方形个数 | 4 | 7 | 10 | 13 | 16 | … |
则剪了n次后共有 个正方形
20、如图是某城市部分街道示意图，AF//BC，AB//ED，BD//AE，
于点C，假设两公交车速度相同，途中耽误时间相同。一路路线为
，二路路线为
。那么一路车比二路车
到达F站？（填“先或后或同时”）
三、用心解一解（共60分）
21、解方程（10分）
（1）
（2）
＋
＝3．
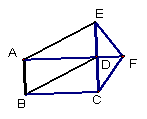
22、(6分) 如图矩形ABCD中,AC与BD交于O点,
BE⊥AC于E, CF⊥BD于F,
求证:BE=CF
23、(6分)工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
(2)摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是 。
(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是
。
|
(图①) (图②) (图③) (图④)
24、(7分)人本超市用50000元从外地购回一批T恤衫,由于销路好,商场又紧急调拨18.6万元采购比第一次多2倍的T恤衫,但第二次比第一次进价每件贵12元,商场在出售时统一按每件80元的标价出售,为了缩短库存时间,最后的400件按6.5折处理并很快售完,求商场在这两次生意中共盈利多少元.
25、（8分）如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，以格点为顶点分别按下列要求画三角形和平行四边形。
（1）使三角形三边长为3，
，
。
（2）使平行四边形有一锐角为45°，且面积为4。
（1） （2）
26、（11分）阅读下面材料，并解答下列问题：
在直角三角形中，a、b表示两条直角边，c表示斜边，勾股定理可以表述为a2+b2=c2。 满足这个等式的正整数a、b、c叫做一组勾股数。 例如（3、4、5），（5、12、13），（6、8、10）等等， 几千年来，人们对勾股数进行了不断的研究和探索，并探索出很多确定勾股数的方法，下面是人们发现的两种方法：
（1）如果m表示大于1的整数，a=2m，b=m2-1，c=m2+1那么a，b，c就是一组勾股数。
（2）若m表示大于1的奇数，把m平方后拆成相邻的两个整数，那么奇数与这两个整数也构成一组勾股数。
问题：（1）判断上面方法是否正确，并选择其中一个你认为对的加以证明。
（2）根据上面材料，你能找出包含23的一组勾股数吗？
（3）你还能找出另外一种确定勾股数的方法吗？请把它表示出来（只要求写出一种）。
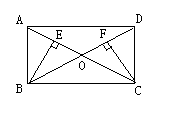
27、（12分）如图，正方形OABC的面积为9，点O为坐标原点，点B在函数y=
(k>0,x>0)的图象上，点P（m, n）是函数y= (k>0,x>0)的图象上任意一点，过点P分别作x轴、y轴的垂线，垂足分别为E、F，并设矩形OEPF和正方形OABC不重合部分的面积为S。（提示：考虑点P在点B的左侧或右侧两种情况）
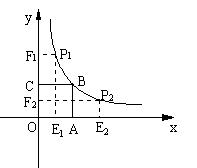（1）求B点坐标和k的值；
（2）当S= 
时，求点P的坐标；
（3）写出S与m的函数关系式。
卷尾语：祝贺你完成了本卷，再仔细检查一下吧，争取最好！