初二数学月考试卷
（满分120分，考试时间100分钟） 2006、5、16
一、 选择题；（每小题3分，共30分）
1、 已知：菱形的一条对角线与边长相等，则菱形的邻角的度数分别为 （ ）
A、450，1350 B、600，1200 C、900，900 D、300，1500
2、以边长5cm，4cm，7cm的三条线段中的两条为边，另一条为 对角线画平行四边形，可以画出形状不同 的 平行四边形的个数 （ ）
A、1 B、2 C、3 D、4
3、已知：在Rt△ABC中，∠ACB=900，周长为24，M是AB的中点且MC = 5，则
△ABC的面积为 （ ）
A、30 B、24 C、16 D、12
4、三角形三边长分别为a、b、c且满足（a - b）（a2+ b2- c2）= 0 ，则该三角形的形状为 （ ）
A、任意等腰三角形 B、任意直角三角形
C、等腰三角形或直角三角形 D、等腰直角三角形
5、三角形三边长分别为2n2+2n， 2n+1， 2n2+2n+1（n为正整数）这样的三角形
（ ）
A、锐角三角形 B、直角三角形
C、钝角三角形 D、钝角三角形 或直角三角形
6、菱形具有而矩形不具有的性质是 （ ）
A、四条边都相等 B、四个角都相等
C、对角线相等 D、对角线平分内角
7、正方形具有而菱形不具有的性质是 （ ）
A、对角线互相垂直平分 B、内角之和为3600
C、对角线相等 D、对角线平分内角
8、正方形的边长为10cm，则以它的对角线为边的等边三角形的面积为（ ）
A、50
cm2
B、25 cm2 C、50
cm2 D、100
cm2
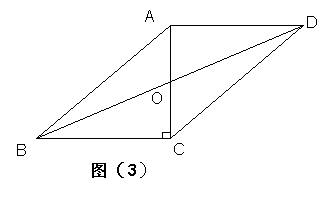9、若x、y的值都扩大为原来的2倍，则分式
的值
（ ）
A、扩大2倍 B、扩大3倍 C、扩大6倍 D、不变
10、若反比例函数y=
经过（ －1，2 ），则一次函数y=－kx + 2的图象一定不经过
（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
二、填空题：（每小题3分，共30分）
1、有一组 的平行四边形叫做菱形，对角线 的平行四边形叫做菱形。
2、菱形ABCD中，AC =AB BD =24cm ， 则点A到CD的距离是 cm，菱形的周长是 cm，菱形的面积是 cm2
3、顺次连结矩形四边的中点所得的 四边形是 ；
顺次连结菱形四边的中点所得的 四边形是 。
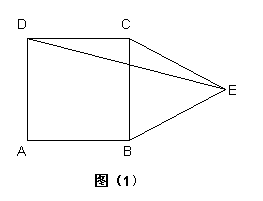
4、如图（1）在正方形ABCD外，以BC为边作等边三角形BCE，
则∠DEC=
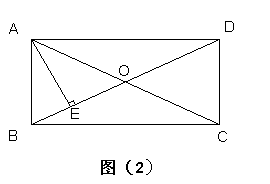
5、如图（2）矩形ABCD中，对角线交于点0，AE⊥BD于E，若BE = OE = 2，
则AC=
6、在△ABC中，∠C=900，若a =8 ，b =6，则c = ；若a =8 ，c =17，则
b = 。
7、直角三角形两直角边的长分别为5和12，则斜边上的高为 。
8、直角三角形两直角边的比为3 ：4，斜边为20，则它的面积为 。
9、已知三角形的三边长为5、12、13，则三角形的面积为 。
10、以下列各组数为边长：（1）3、4、5、（2）10、12、13（3）5、12、13
（4）15、20、25其中能构成直角三角形的序号是
三、按要求回答问题：（每小题10分，共60分）
1、如图（3）：四边形ABCD是平行四边形，AB =10 ，AD =8，AC⊥BC，求BC、CD、AC、OA的长以及平行四边形ABCD面积。
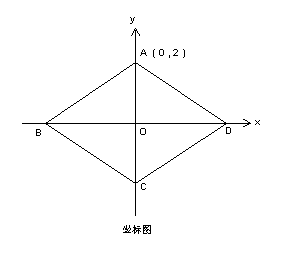
2、 在平面直角坐标系中，四边形ABCD是菱形，∠ABC=600 ，点A的坐标为
（0 ，2），求点B、C、D的坐标。
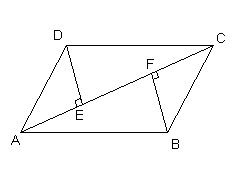
3、 如图：在四边形ABCD中，AD = BC ，AF = CE，DE⊥AC，BF⊥AC，
求证：四边形ABCD是平行四边形
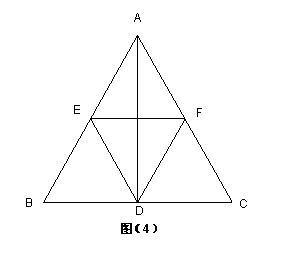
4、 如图：在△ABC中， AD⊥BC 于D， E、F、分别是AB、AC边的中点，连结DE、EF、FD，当△ABC满足什么条件时，四边形AEDF是菱形 ，并证明。
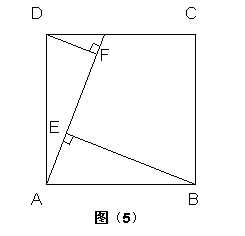
5、 如图；正方形ABCD中，点P是CD上一点，BE⊥AP于E，DF⊥AP于F
求证；AE = DF
|
6、 观察探索题：
方程x + 
= 2 + 
① 的解是x 1 = 2 ，x2
=
方程x + = 3 + 
① 的解是x 1 = 3， x2 =
方程x + = 4 +
① 的解是x 1 = 4， x2 =
（1）
观察上述方程后，解关于x的方程x + = 
化成方程（1）的形式 ，可猜想方程的解是
（2）
把关于x的方程x + 
=
（a是常数且a≠0）
化成方程①的形式，并求出方程的解。