八年级数学试卷
班级 姓名 得分
一、填空题（每空2分，共42分）
1、
的平方根是
；
2、如图，△ABC为等边三角形，边长为2cm，D为BC中点，△AEB
是△ADC绕点A旋转60°得到的，则∠ABE＝＿＿＿度；BE＝＿＿＿。
若连结DE，则△ADE为__________三角形。
3、化简：
；
；
4、比较大小：
；
；（用“>”或“<”填空）。
5、计算：
；
=
；
6、估算：
=
（误差小于0.1）；
=
（误差小于1）。
7、利用计算器计算：
（结果保留三位有效数字）。
8、在棱长为
的正方体木箱中，想放入一根细长的铁丝，
则这根铁丝的最大长度可能是 ；
9、面积为13的正方形的边长是 。
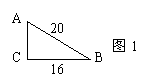
10、如图1，△ABC中，∠C =90º，AB =20，BC =16，则AC = 。
11、△ABC中，∠C =90º，∠A、∠B、∠C所对的边分别是a,b,c,若a=8，c=17，则b= 。
12、三角形的三边分别为7，15，24，则这个三角形的最大角为 度。
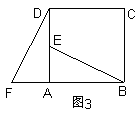13、如图2，∠DEF是∠ABC经过平移得到的，∠ABC=35º，
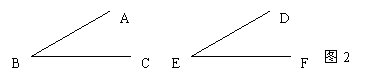则∠DEF= º
14、如图3，通过平移、轴对称、旋转中的哪一种方法可使△ABE变到△ADF的位置。答： 。
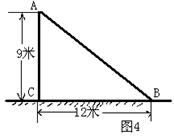
15、如图4，一根电线杆因超过使用寿命被大风刮倒了，折断处离地面9米，电线杆顶部在离电线杆底部12米处，这根电线杆在折断前有 米。
二、选择题（每题3分，共21分）
1、以下列各组数为边的三角形不是直角三角形的是（ ）
A、24，10，26 B、5，3，4 C、60，11，61 D、5，6，9
2、下列各数中，有理数的个数为（ ）
；
；0.999……；
；0 ；
；
；
；
；
A、3 B、4 C、5 D、6
3、下列说法中不正确的是（ ）
A、－1的立方根是－1。 B、0的平方根与立方根相等。
C、－4的平方根是
。 D、每个数都有一个立方根。
4、下列各式估算正确的是（ ）
A、
B、
C、
D、
5、下列各式中正确的是（ ）
A、
B、
C、
D、
6、下列六种说法正确的个数是 ( )
(A) 1 ( B) 2 (C) 3 (D) 4
1无限小数都是无理 2正数、负数统称有理数 3无理数的相反数还是无理数 4无理数与无理
数的和一定还是无理数 5无理数与有理数的和一定是无理数 6 无理数与有理数的积一定仍是无理数
7、下列四个图形中，不能通过基本图形平移得到的是（ ）
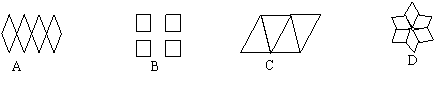
三、解答题（共57分）
1、（9分）化简：
（1）
（2）
（3）
2、（5分）小明房间的面积为10.8㎡，房间地面恰巧由120块相同的正方形地砖铺成，每块地砖的
边长是多少。
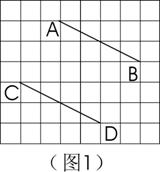
3、(1)（3分）把小船ABCD通过平移后到
的位置，请你根据题中信息，画出平移后的小船位置。(2)(2分)如图1，线段CD是线段AB经过向左平移______格，再向下平移______格后得到的。
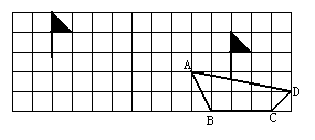
4、（6分）按要求分别画出旋转对称图形：
（3）画△ABC绕O点顺时针方向旋转90°后得到△
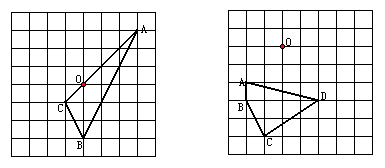（4）把四边形ABCD绕O点逆时针方向旋转90°后得四边形。
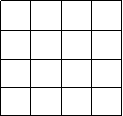
5、（7分）如图，正方形网格中的每个小正方形边长都是1，任意连结这些小正方形的顶点，可得到一些线段。请在图中画出
这样的线段，并选择其中的一个说明这样画的道理。
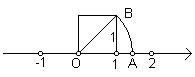6、（8分）我们在学习“实数”时，画了这样一个图，即“以数轴上的单位长为‘1’的线段作一个正方形，然后以原点O为圆心，正方形的对角线长为半径画弧交x 轴于点A”，请根据图形回答下列问题：
（1）线段OA的长度是多少？（要求写出求解过程）
（2）这个图形的目的是为了说明什么？
（3）这种研究和解决问题的方式，体现了 的数学思想方法。
（将下列符合的选项序号填在横线上）
A、数形结合 B、代入 C、换元 D、归纳
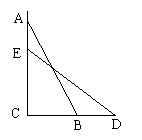7、（8分）如图，一个梯子AB长2.5
米，顶端A靠在墙AC上，这时
梯子下端B与墙角C距离为1.5米，梯子滑动后停在DE的位置上，测
得BD长为0.5米，求梯子顶端A下落了多少米？
8、阅读下列短文，回答有关问题：
在实数这章中，遇到过、
这样的式子，我们把这样的式子叫做二次根式，根号下的数叫做被开方数。如果一个二次根式的被开方数中有的因数能开的尽方，可以利用
将这些因数开出来，从而将二次根式化简。当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分数时，这样的二次根式叫做最简二次根式，例如，
化成最简二次根式是
，
化成最简二次根式是
。几个二次根式化成最简二次根式以后，如果被开方数相同，这几个二次根式叫做同类二次根式，如上面的例子就是同类二次根式。
（1）请判断下列各式中，哪些是同类二次根式？
（2）二次根式中的同类二次根式可以像整式中的同类项一样合并，请计算：
