八年级下数学阶段性测试卷（问卷）
一、选择题：（每小题3分，共30分）
1、下列二次根式中，与
是同类二次根式的是（ ）
A．-
B．-2
C．3
D．
2、已知点P（a,b），点P关于y轴对称的点的坐标为（ ）
A.(a,-b) B.(-a,b) C.(-a,-b) D.( b,a)
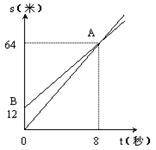
3、如图：OA、BA分别表示甲、乙两名学生运动的一次函数图像，图中s和t分别表示运动路程和时间，根据图像判断快者的速度比慢者的速度每秒快（ ）
（A）2.5米 （B）2米 （C）1.5米 （D）1米
4、若b < 0，化简
的结果是（ ）
A、
B、
C、
D、
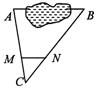
5、如图，A、B两点被池塘隔开，在AB外任选一点C，连结AC、BC分别取M、N，使得AM=2MC，BN=2NC，这时有AB∥MN．量得 MN＝38m．则AB的长是
（A） 152m （B）114m （C）76m （D）104m
6、下列函数中自变量x的取值范围是x
2的是( )
（A）y=
（B）
（C）y=
（D）
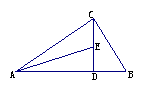7、如图，已知∠ACB=90°，CD⊥AB，∠B=60°，AE是∠CAD的平分线，若将∠EAD用放大镜放大两倍，则放大后的角的大小为（ ）
（A）∠EAC的大小 （B）∠DCB的大小
（C）∠B的大小 （D）∠ACB的大小
8、已知一次函数y = kx + b，当–3≤x≤1 时，对应的y的值为1≤y≤9，则kb的值为（ ）
A．4 B．– 6 C．– 4 或21 D．– 6 或14
9、已知
，则锐角的取值范围是（ ）。
A、0°<
< 30° B、30°<< 45° C、45° <<60° D、60°<<90°
10、如图,在平行四边形ABCD中,O1、O2、O3分别是对角线BD上的三点，且BO1=O1O2=O2O3=O3D，连接AO1并延长交BC于点E，连接EO3并延长交AD于点F，则AF：DF等于
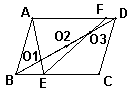(A)19:2
(B)9:1
(C)8:1 (D) 7:1
二、填空题：（每小题3分，共30分）
11、甲、乙两个立方体铁块的边长比为2:1，若甲铁块沉入盛水的量杯中，水面上升2.4cm。则甲、乙两铁块同时沉入杯中时，水面应升高 。
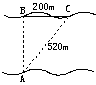
12、如图，某人欲横渡一条河，由于水流的影响，实际上岸地点C偏离欲到达点B200m，结果他在水中实际游了520m，则该河流的宽度为_________。
13、运动会入场式中，一个方队共有n人，这个方队最外面一周共有 人。
14、若
= 1，则锐角的度数是 。
15、从A地向B地打长途电话按时计费，3分钟内收费2.4元，超过3分钟每增加1分钟加收1元，求时间t≥3（分）时电话费y (元)与时间t之间的函数关系式为 。
16、如图：已知：a<
b , b+c>0,化简：
－
＋
＝
。
a b O c
17、函数
的图象交于一点，这个点坐标是
。
18、如图，在下面条件中能使△ACD∽△ABC的条件序号为 。
①
；②
；③
；④
19、如图，在菱形ABCD中，AE⊥BC于E，EC=1，sinB=
，则四边形AECD的周长为__________。
20、如上图，A、B为两个新建生活小区，它们位于公路CD的同侧（沿公路CD已铺有宽带网）．现要从公路CD上找一处接点，向A、B两个小区铺设宽带网．铺设工程费用为25000元/千米，已知AC=4km，BD=1km，CD=4km，则最少花费 元（结果保留整数）即可完成铺设工程。
三、解答题：
21、（6分）计算或化简：
（1）
（2）
22、（7分）一条弹簧它所能挂的重量不能超过10千克，在这个范围内，弹簧的长度y与所挂物体的重量x的关系可表示为y = kx + b（k、b是常数且k≠0），这条弹簧所挂的重是为2千克时，弹簧长14厘米；当所挂的重物为5千克时，弹簧长17厘米，求：
（1）k、b的值，写出函数的解析式； （2）作出这个函数关系的图像；
（3）求当挂重物4千克时弹簧的长度； （4）求自变量x的取值范围。
23、（7分）已知Rt△ABC中，∠C = 90°，a、b分别是∠A、∠B的对边，且满足a2 – 3ab = 0，求tanA。
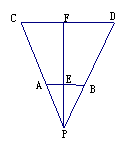24、（7分）一条河的两岸有一段是平行的。在河的一岸每相距5米栽一棵树,在河的对岸每相距50米架一根电线杆。在栽树的一岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽（如图，已知AB∥CD，PF⊥CD于F，交AB于E，AB=20，CD=50，PE=25，求EF的长）。
 |
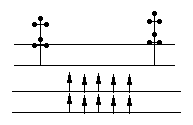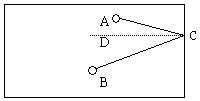25、（7分）在釜山亚运会上，斯诺克（台球）是一个比赛项目。你知道吗？台球在运动时有这样的规律：当球在运动过程中碰到台壁时，将以一定的角度反弹。如图所示：
现在在球台中有一个白球A，要通过打右台壁反弹到红球B。A距离右台壁1.5米，B距离右台壁2米；A距离上台壁0.25米，B距离下台壁0.4米。标准桌子的宽度为2.05米。问白球打到右台壁什么位置处，刚好能经过一次反弹击中红球？
26、（8分）如图，四边形ABCD中，两对角线互相垂直。试说明：AB2 + CD2 = BC2 + AD2。
 |
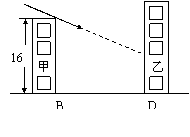
27、（8分）如图，甲楼高16米，乙楼坐落在甲楼的正北面，已知当地冬至中午12时太阳光线与水平面的夹角为30°，此时，求：（1）如果两楼相距20米，那么甲楼的影子落在乙楼上有多高？（2）如果甲楼的影子刚好不落在乙楼上，那么两楼的距离应当是多少米？
 |
28、（10分）南方A市欲将一批容易变质的新鲜水果运往B市销售，共有飞机、火车、汽车三种运输方式。现只可选择其中的一种，这三种运输方式的主要参考数据如下表所示：
| 运输工具 | 途中速度 （千米/小时） | 途中费用 （元/千米） | 装卸费用 （元） | 装卸时间 （小时） |
| 飞机 | 200 | 16 | 1000 | 2 |
| 火车 | 100 | 4 | 2000 | 4 |
| 汽车 | 50 | 8 | 1000 | 2 |
若这批水果在运输（包括装卸）过程中的损耗为200元/小时，设A、B两市间的距离为x千米，
（1）如果用W1、W2、W3分别表示使用飞机、火车、汽车运输时的总支出费用（包括损耗），求出W1、W2、W3与x间的函数关系式；
（2）应采用哪种运输方式，才使运输时的总支出费用最小？