18章勾股定理复习练习三(无答案）

八年级数学（下）第18章勾股定理复习练习三

　　　　　　　　 姓名_______　　　　　班级_______　

一、相信你一定能选对！

1. 下列三角形中是直角三角形的是（　　　 ）

A.三边之比为5∶6∶7　　　　 　　　　　　 B.三边满足关系a+b=c　

C.三边之长为9、40、41　　　 　　　　　　 D.其中一边等于另一边的一半

2．直角三角形有一条直角边为6，另两条边长是连续偶数，则该三角形周长为（　　 ）

　 A. 20　　　　　 　　B.　22　　　　 　　　 C.  24　　　　　　 D.　26

3．直角三角形中，周长为2+，斜边上的中线为1，则此直角三角形的面积为（　　）

A、2　　 B、　　 C、4　　  D、

4. 如图，有一块直角三角形纸片，两直角边AC=6cm,

BC=8cm,现将直角边AC沿直线AD折叠，使它落在斜边

AB上，且与AE重合，则CD等于（　 ）

(A) 　 (B)　　 (C)　　(D)

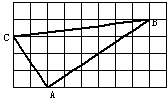5. 如图，正方形网格中的△ABC，若小方格边长

为1，则△ABC是 （　 ）

(A)直角三角形　 (B)锐角三角形

(C)钝角三角形　 (D)以上答案都不对

6.在△ABC中，AB=15,AC=13,高AD=12,则三角形的周长是　　　 （　　）

（A） 42　　 (B) 32 　 (C) 42或32　(D) 37或33.

7.小强量得家里新购置的彩电荧光屏的长为58厘米,宽为46厘米,则这台电视机的尺寸是(实际测量的误差可不计)　(　　)

(A).9英寸(23厘米)　　 (B).21英寸(54厘米)

 (C).29英寸(74厘米)　　(D).34英寸(87厘米)

8．在△ABC中，已知AB=12,AC=9,BC=15则△ABC的面积等于　(　　)

A.108　　　　　 B.54　　　　　  C.180　　　　　 D.90

9．若直角三角形的两条直角边各扩大1倍,则其斜边扩大　　　　　　　　　　　　　  (　　 )

A.倍　　　　  　　　　 B.1倍　　　　　　　  C.2倍　　　　　　 D.倍

10．一个三角形三边之比为3∶4∶5,则这个三角形三边上的高之比为　　　　　　　　  (　　 )

A.3：4：5　　　　　　　  B.5：4：3　　　　　 　C.20：15：12　　 　D.10：8：2　

二、你能填得又快又对吗？

11．现有两根长分别是3cm和4cm木棒，若要钉成一个直角三角形木架,第三根木棒最短长是_______cm

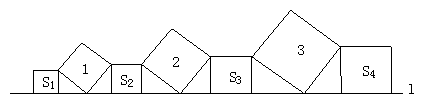
12、在直线l上依次摆放着七个正方形(如图所示)。已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S₁、S₂、S₃、S₄，求S₁＋S₂＋S₃＋S₄的值：_______________

13．正方形的对角线为4，则它的边长AB=　　　.

14．如果梯子的底端离建筑物9米，那么15米长的梯子可以到达建筑物的高度是______米.

15．一座桥长15米，一艘小船自桥北头出发，向正南方向驶去，因水流原因，到达南岸后，发现已偏离桥南头9米，则小船实际行驶了　　　　  米。

16．如图，把一张长方形纸片ABCD折叠起来，使其对角顶点

（第16题）

A，C重合，折痕为EF。若AB＝1，BC＝2，则AF＝　　　

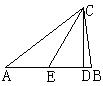图2　　　　图3　　　　　　

17.在Rt△ABC中, ∠C=90°,AB=15,BC:AC=3:4,则BC=　　 .

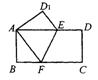
18.如图2，∠OAB=∠OBC=∠OCD=90°， AB=BC=CD=1，OA=2，则OD²=　　　　.

19.小明把一根70cm长的木棒放到一个长、宽、高分别为30cm、40cm、50cm

的木箱中，他能放进去吗？答：　　　 　 .（填“能”、或“不能”）

20.如图3，在△ABC中，CE是AB边上的中线，CD⊥AB于D,且AB=5,BC=4,

AC=6,则DE的长为　　　　　 .

三、认真解答，一定要细心哟！

21．作图题：在数轴上作出表示的点.（保留作图痕迹，不写作法，但要作答）

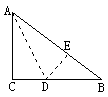
22．已知：如图，已知∠B=∠D=90°，∠A=60°，AB=10，CD=6。

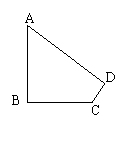求：四边形ABCD的面积。

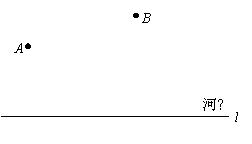
23．如图，要在河边修建一个水泵站，分别向张村A和李庄B送水，已知张村A、李庄B到河边的距离分别为2km和7km，且张、李二村庄相距13km．

（1）水泵应建在什么地方，可使所用的水管最短？请在图中设计出水泵站的位置；

（2）如果铺设水管的工程费用为每千米1500元，为使铺设水管费用最节省，请求出最节省的铺设水管的费用为多少元？

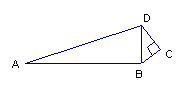24．在四边形ABCD中，AB=12cm，BC=3cm，CD=4cm，∠C=90⁰。求：

（1）BD的长　 （2）当AD为多少时，∠ABD=90⁰ 。

25．如图，已知四边形ABCD的对角线AB⊥CD于O，请说明AC²＋BD²＝AD²＋BC²的理由。

　　

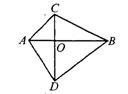
 （第25题）

26.“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过千米/小时，如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路面对车速检测仪正前方米处，过了秒后，测得小汽车与车速检测仪间距离为米，这辆小汽车超速了吗？

27.如图，在一块由边长为的地砖铺设的广场上，一只飞来的鸽子落在点处，，鸽子吃完小朋友洒在、处的鸟食，最少需要走多远？

28．如图是美国总统Ｇarfield于1876年给出的一种验证勾股定理的办法，你能利用它验证勾股定理吗？请做一做．

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　

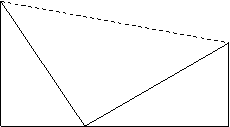b　　　  c　　　　　　 c

　　　　　　　　　　　　　　　　　　

 a　　　　　　　　 b