八年级下数学第17章《反比例函数》练习题一
班级_______ 姓名_______ 学号▁▁▁
一、填空题：
1、反比例函数
的图象经过（－
，5）点、（
）及（
）点，
则
＝
，
＝
，
＝
；
2、若反比例函数
的图象经过二、四象限，则=
_______
3、已知
-2与
成反比例，当=3时，=1，则与间的函数关系式为
；
4、已知正比例函数
与反比例函数
的图象都过A（
，1），则＝ ，正比例函数与反比例函数的解析式分别是
、
；
5、设有反比例函数
，
、
为其图象上的两点，若
时，
，则的取值范围是___________
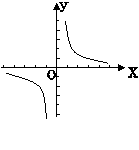
6、如图是反比例函数的图象，
则k与0的大小关系是k 0.
7、函数
的图象，在每一个象限内，
随的增大而
；
8、反比例函数
在第一象限内的图象如图，
点M是图象上一点，MP垂直轴于点P，如果△MOP的
面积为1，那么的值是
；
9．已知点A（
,
）在第二象限，且m为整数，
则过A的反比例函数的关系式为__________________.
10．正比例函数
的图象与反比例函数
的图象的一个交点是A，点A的横坐标是2，则此反比例函数的关系式为_________________.
二、选择题
11、下列函数中，是反比例函数的是（ ）
A. 
B.
C. 
D.
12、 函数
与
（
）的图象的交点个数是（ ）
A. 0 B. 1 C. 2 D. 不确定
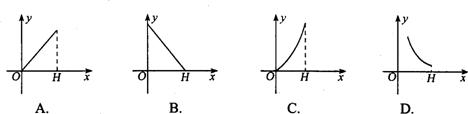
13．向高为H的圆柱形水杯中注水，已知水杯底面半径为2，那么注水量y与水深x的函数图象是 ( )
14．面积为4的矩形一边为，另一边为y，则y与x的变化规律用图象大致表示为 （ ）
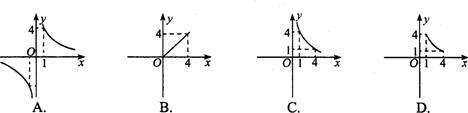
15．已知点P1(a，b)在函数(k≠0)的图象上，那么不在此图象上的点是（ ）
A．P1(b，a) B．P2(－a，－b)
C．P３(－b，－a) D．P4(－
，－
)
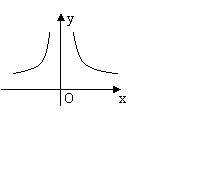
16．如图所示的图象的函数关系式只能是（ ）
A. 
B.
C. 
D.
17．在函数
(k＞0)的图象上有三点A1(x1, y1 )、A2(x2, y2)、A3(x3, y3 ),已知x1＜x2＜0＜x3,则下列各式中,正确的是 ( )
A.y1＜y2＜y3 B.y3＜y2＜y1 C. y2＜ y1＜y3 D.y3＜y1＜y2
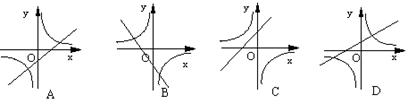
18.如图，函数y＝k（x＋k）与在同一坐标系中，图象只能是下图中的（ ）
 |
19、若与－3成反比例，与
成正比例，则是
的（ ）
A、 正比例函数 B、 反比例函数 C、 一次函数 D、 不能确定
20、若反比例函数
的图象在第二、四象限，则的值是（ ）
A、 －1或1 B、小于
的任意实数 C、 －1 Ｄ、 不能确定
三、解下列各题
21、（8分）已知函数
，其中
成正比例,
成反比例,且当
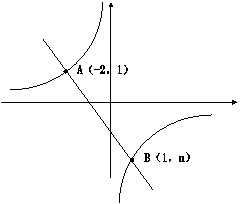
22、（8分）如图，一次函数
的图象与反比例函数
的图象相交于A、B两点，（1）利用图中条件，求反比例函数和一次函数的解析式（2）根据图象写出使一次函数的值大于反比例函数的值的的取值范围.
23．建筑工地上有一堆圆锥形沙堆，其底面积为60 m2，高为4 m．
(1)沙堆的底面积S与沙堆的高
有怎样的函数关系?
(2)为使工地运输方便，决定将沙堆的占地面积减少5 m2。，这时沙堆的高为多少?(精确到0.1 m)
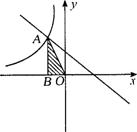24．如图，Rt△AOB顶点A是一次函数
的图象与反比例函数
的 图象在第二象限内的交点，且S△AOB＝1，求A点坐标．
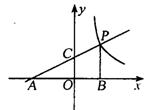25．直线
分别交x、y轴于点A、C，而P是该直线上在第一象限内的一点，PB⊥轴，B为垂足，S△ABP＝9．
(1)求点P的坐标．
(2)求经过P点的反比例函数的解析式．
26．某年上年度电价为0.8元，年用电量为1亿度，本年度计划将电价调至0.55～0.75 元之间．经测算，若电价调至x元，则本年度新增用电量y(亿)度与(x—0.4)(元)成反比例．当
时，
．
(1)求y与x之间的函数关系式．
(2)若每度电的成本价为0.3元，则电价调至多少元时，本年度电力部门的收益将比上年度增加20％．[收益＝用电量×(实际电价一成本价)]
附答案：1、-7.5，2.5，-0.75，2、0，3、
，4、3，5、k＜-1,6、k＞0，
7、增大，8、2，9、
，10、
。
二、BAACD DCDAC
三、21、
，22、，y=-x-1,当x＜-2或0＜x＜1,23、
，h≈4.4
24、A(-1,2) ,25、P(2,3), 
, 26、
，0.6元。