一、知识回顾
1.不等式的基本性质1：不等式的两边都加上（或减去）同一个 ，不等号的方向 。
2.不等式的基本性质2：不等式的两边都乘以（或除以）同一个正数，不等号的方向 ；不等式的两边都乘以（或除以）同一个负数，不等号的方向 。
3.用不等式表示：（1）a的绝对值是非负数： ；（2）x的5倍与2的差不大于1： ；（3）x与13的差比它的8倍小： 。
4.用不等号连接：（1）
，则x 
；（2）若
，则
；（3）若>则
。
5.满足不等式
的负整数解是
。
二、典型例题
1.求下列不等式，并把解集在数轴上表示出来（注意选择解法，使计算量尽可能地小）
（1）
（2）
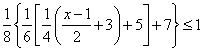
2.求关于x的不等式
的解集
3. 已知方程组
的解
与
的两倍之差为负数，求的值
4.一个工程队原定10天内至少要挖掘600立方米的土方，在前两天共完成了120立方米，又要求提前2天完成挖掘任务，问以后几天内，平均每天至少要挖掘多少土方？
一、知识回顾
1. 用不等式表示：x的一半比－5大，且比3小：
2.
如果，则（1）
的解集为
； （2）
的解集为
； （3）
的解集为
； （4）
的解集为
。
3.
不等式组
的解集是
；
4.
x取值为
时，一次函数
的值大于
的值。
5. 一个两位数，十位上的数比个位上的数小2，如果这个两位数大于37且小于58，则这个两位数为 。
二、典型例题
1. 解下列不等式组：
（1）
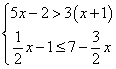（2）
2.
若不等式组
的解集是
，求
的取值。 3. 若关于x的不等式组
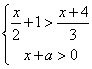
的解集为
，试求的取值范围
3. 用若干辆载重量为8吨的汽车运一批货物，若每两汽车只装5吨，则剩下10吨货物，若每辆车装8吨货物，则最后一辆车不空也不满，请问有多少辆汽车？
1.
不等式
的解集为
，那么m
2.
如果关于x的方程
的解是3，则不等式
的解是
3.
方程
的解有 个，不等式
的解有 个，其中非负整数有 个
4.
已知
，
，那么、
、
之间的大小关系为
5.
满足不等式
的整数解是
6.
直线
与坐标轴的两个交点分别为A
、B
，则不等式
的解为
7.
若不等式组
无解，则的取值范围是
8.
函数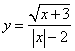
中的自变量的取值范围是
9.
已知直线经过第一、二、三象限，且与x轴交于点（－4，0），则当
时，的取值范围是
10. 已知⊿ABC中，三边分别为a、b、c，且a=2c，则⊿ABC中的最短边是
11.
（1）求不等式
的非正整数解
（2）解不等式组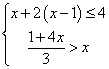
12. 水果店进了某种水果2000千克，进价每千克7元，出售价格为每千克11元。销售一半后，为尽快销售完，准备打折销售。如果要使总利润不低于6900元，那么余下的水果可按原定价打几折出售？
13. 初二年级夏令营，若租用45座客车若干辆，则刚好坐满，若租用54座客车，则能少租2辆，且有一辆没有坐满，但超过三分之二，你能知道初二年级有多少学生参加夏令营吗？若租用45座客车每辆250元，租用54座客车每辆300元，你知道怎样租车比较合算吗？