因式分解
一、 填空题：（每小题2分，共24分）
1、 把下列各式的公因式写在横线上：
①
=
；
②
= 
2、 填上适当的式子，使以下等式成立：
（1）
（2）
3、 在括号前面填上“＋”或“－”号，使等式成立：
（1） 
；
（2）
。
4、 直接写出因式分解的结果：
（1）
；
（2）
。
5、
若
6、
若
，那么m=________。
7、
如果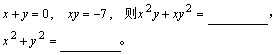
8、
简便计算：
9、
已知
，则
的值是
。
10、如果2a+3b=1,那么3-4a-6b= 。
11、若
是一个完全平方式，则
的关系是
。
12、已知正方形的面积是
（x>0，y>0）,利用分解因式，写出表示该正方形的边长的代数式
。
二、 选择题：（每小题2分，共20分）
1、下列各式从左到右的变形中，是因式分解的为（ ）
A、
B、
C、
D、
2、一个多项式分解因式的结果是
，那么这个多项式是
（ ）A、
B、
C、
D、
3、下列各式是完全平方式的是（ ）
A、
B、
C、
D、
4、把多项式
分解因式等于（ ）
A
B 
C、m(a-2)(m-1) D、m(a-2)(m+1)
5、
因式分解的结果是
（ ）A、
B、
C、
D、
6、下列多项式中，含有因式
的多项式是（ ）
A、
B、
C、
D、
7、分解因式
得（ ）
A、
B、
C、
D、
8、已知多项式
分解因式为
，则
的值为（ ）A、
B、
C、
D、
9、在边长为a的正方形中挖掉一个边长为b的小正方形（a>b）。把余下的部分剪拼成一个矩形（如图）。通过计算图形（阴影部分）的面积，验证了一个等式，则这个等式是（ ）
A、
B、
C、
D、
三、 将下列各式分解因式
（1）
（2）
（3）
（4）
（5）
四、 解答题及证明题（每小题7分，共14分）
1、
已知
，求
的值。
2、
利用分解因式证明：
能被120整除。
3、已知
是△ABC的三边的长，且满足
，试判断此三角形的形状。（6分）